Sound Waves

The sound, as physical appearance, can propagate only in material and elastic environment or medium, like air, water, wood or any other firm body. When there is a change in a stationary state of the particles that medium consists of, then that's called a acoustic oscillations. This change in state is manifested as change in the pressure or the density of the medium. The source of sound causes that change and it spread it with proper speed in the space as a sound waves.

The sound waves can be longitudinal or transverse waves. For example, if small ball changes its volume, then it will suppress the molecules of the air around it. That way, the density of the air molecules is increased and they start to suppress the adjacent layers of the air. This process generates changes in pressure in the space, and that's called sound field. The pressure in one point of the space is changing depending on time and space coordinate of that point. The air molecules are not displaced, but their movement is transmitted around the stationary state. As the sound wave is spreading, its intensity decreases, because the energy also decreases by unit volume of the space in which sound wave propagates.

The range of sound that man can hear is from 20 Hz to 20 kHz. The waves at frequency lower than 20 Hz are known as infra-sound, while the waves at frequencies higher than 20 kHz belong to the so called ultra-sound. The propagation of all these sound waves is under the same laws.

Depending on the frequency spectrum of the sound wave, we can distinguish three types of sound:

>> Simple sound - single frequency wave;
>> Complex sound - multiple frequencies wave;
>> Non-periodic sound - or noise;

The pressure intensity of each type of sound depending on frequency looks like the plots shown on Picture 1.

Picture 1: Pressure of sound in frequency domain: A. Simple sound; B. Complex Sound; C. Noise;


The pressure intensity of each type of sound depending on frequency, looks like the plots shown on Picture 1. The simple sound consists of one single frequency, so the plot has just one amplitude shown on current wave frequency, plot A. The complex sound shown on plot B, consists of three different frequencies, the major part is on f1, the next two are for one octave higher, 2*f1 and 3*f1, respectively. Finally, on plot C is shown the pressure of the noise sound wave depending on frequency. As it can be seen, it has some frequency range where its pressure amplitudes varies with different values, randomly.

Utilization of Radio Waves Energy

The method of utilization of the radio waves energy is kind of a derived idea from the Tesla's Method Of Utilizing Radiant Energy, as general concept. In this article, we analyze one simple electronic circuit which can be used as simple prototype for proving the concept of utilization of the energy of radio waves which propagates in the Earth's atmosphere all the time. These radio waves does not have a mysterious origin at all, as it can be found in many places on the internet sites which treats the so called "free energy" phenomenon. On the contrary, these radio waves are just real and known, human made signals. They origin from the base and repeater stations of the broadcasting network, comprising emitters of all local and national radio stations. The signal emitted from your favorite radio station which broadcasts program with music and news of your interest, is always present in the air around you, no matter if you catch that signal on your radio and listen its live program, or your radio is turned off. That signal is always there. And not just the signal from that particular radio station, which is your favorite, but also and all the other stations that emit their signals in your near or far environment.

So, if you chose not to listen the radio, that doesn't mean that you can not catch the radio signals around you, and try to utilize or store the energy that they carry out with them. Although this energy is relatively small, it can still be detected and accumulated on proper way, just as a proving fact that it exists in the air. Furthermore, since we know the origin of these radio waves, we can't say that the energy they carry around is "free", because we know that this energy is generated in the transmitter stations of the radio service which generated it. These radio transmitters doesn't work from nothing, they use electric power to generate the needed EM energy of the radio waves which they broadcast via the antennas, in their well known and pre-calculated range. Of course, the radio station is paying for the electric energy that it consumes, but the very small portion of the emitted EM energy that comes to your radio receiver via its receiver antenna at your home, you get it for free. However, this received energy is far different from the term "free energy" and its actual meaning.

The receiving circuit for utilizing radio waves energy

Let's now take a look at one real and simple circuit, which can accumulate the EM energy of radio waves via the receiving antenna. The utilization circuit is shown on Picture 1. The electrolytic capacitors C3 and C4 are used as elements for storing the energy, as they accumulate the charge from the incoming small-amplitude radio signals via the diode network which is constructed with 4 diodes D1, D2, D3 and D4, connected as shown in circuit (Picture 1). The capacity of the energy storing capacitors are set to relatively huge value of 1000 μF. The radio signals received from the antenna, are passed to the diode network via the signal block capacitors C1 and C2. Their value is set to 22 nF. Since we are simulating this circuit, we also need to simulate and the antenna as the most important circuit element here.

An antenna is best modeled as a voltage source with a fixed value of internal resistance. Generally, that is the radiation resistance of the antenna. So, in our circuit, we modeled the receiving antenna as a simple voltage source, with the series resistance value of 50 ohms. Although the voltage level of real radio waves is very small, we chose the value of magnitudes in this simulation which is far more higher, just for analyzing purposes. However, the concept of functioning of this circuit and its effect, will remain the same and for smaller and real values for the magnitudes of the incoming radio waves, except that the resulting values of the output voltage V+, will be much smaller, accordingly to the input signal values. But the important thing here, is to see that this idea as concept for utilization of the energy, really works. Therefore, for the antenna model used in our simulation, we use simple sinusoidal wave form, with magnitude of 200 mV at frequency of 500 kHz.

Picture 1: Utilization of Radio Waves Energy (simple circuit)

Time-domain analysis

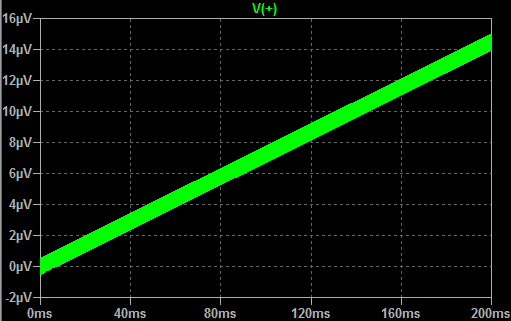
The results of the transient analysis for this circuit in time domain are shown on Picture 2. For this analysis, the same simple sinusoidal wave form, with magnitude of 200 mV at frequency of 500 kHz, is used for antenna signal. As it can be seen from the plot, the output voltage level starts increasing with oscillating wave form, according to the input signal frequency. Starting from zero, the output level reaches value of about 14 μV after time period of 200 ms. The increasing rate is almost linear, so, after time period of 1 second, output will increase to value around 70 μV. This value is about 0.00035% of the input signal magnitude value. In other words, it's far more less than the input. So, in order to achieve really measurable voltage on the output of this circuit, the circuit should work for a long time, thus accumulating energy constantly. We have implemented one real prototype of this circuit, and the real results from practice showed us that the circuit should be left in accumulating mode for, let's say a period of one whole day, in order to achieve a value of several up to hundreds of mV on its output.

Picture 2: Transient analysis - output voltage V+ wave form (time-domain) - for single frequency input


The above results are in case of single-frequency input signal. As we now, in practice, the antenna will receive more than one signal, and all signals will have different frequencies. Furthermore, these signals are not simple and with pure sinusoidal form, since they are modulated in the proper modulation technique for radio transmission. So, the actual input signal received from the real antenna, would be a superposition of all radio signals that the antenna can receive in the environment where it is installed. However, for analysis purposes, we modeled another type of input antenna, which consists three different voltage sources connected in parallel, just to see the effect of the superposition of several signals at different frequencies. In our case, we set these three voltage sources with the following properties:

>> V1 voltage source: Frequency: 500 kHz; Amplitude: 200 mV; Wave form: sinusoidal;
>> V2 voltage source: Frequency: 100 kHz; Amplitude: 200 mV; Wave form: sinusoidal;
>> V3 voltage source: Frequency: 1 MHz; Amplitude: 200 mV; Wave form: sinusoidal;

Picture 3: Transient analysis - output voltage V+ wave form and input signal from Antenna (time-domain) - for 3 inputs at different frequencies

The resulting input signal wave form of the antenna is shown on Picture 3. On same plot is shown and the output voltage V+. As it can be seen, although all three input signals have same magnitude of 200 mV, because of their different frequencies, the resulting signal has amplitudes less then 200 mV. The final effect of this superposition is that the output voltage is increasing with slower rate, comparing with the previous case of one single-frequency input signal. So, after the time period of 200 ms, the output level will reach value smaller than 14 μV, as it reached in the previous case (Picture 2).

AC Analysis

The output voltage AC analysis of this circuit shows that it has higher output level as the frequency of the signal increase. For this AC analysis we set the frequency range of the input signal from 10 KHz to 10 GHz. Taking into account the whole Radio Spectrum which covers frequencies from 3 Hz up to 3000 GHz, this range that we analyze here is pretty much wide. The output voltage level at frequency of 10 KHz is -144 dB and it increases in linear mode up to frequencies of 100 MHz, where it reaches the level of -66 dB. After these frequencies, the output voltage is still increasing, but with slower rate. Finally, for frequencies above 1 GHz it stops to increase and its level remains at about -59 dB. The output level plot in frequency domain is shown on Picture 4.

Picture 4: AC analysis - output voltage V+ level (frequency-domain) - for single frequency input


Also, it's good to mention here, that in the lower frequency range of the radio spectrum, starting from 3 Hz to 10 KHz the output level is decreasing. Namely, at 3 Hz input signal, the output level is around - 100 dB, then it decreases with different speeds as frequency increases, so at frequency of around 3 kHz, it reaches the minimum level of around - 150 dB. For the frequencies above 3 kHz it starts to increase.

From the above analysis, we can conclude that this concept really works, but the amount of accumulated energy is not what we really expect and need in real applications. Since we talk about energy storing, we actually need amount of stored energy enough to power some small consumer, let's say LED diode light, or something else. In any case, this is just a simple approach of this concept. The circuit for utilization can be upgraded and optimized in many ways, in order to achieve better and usable effect in practice. The circuit can be split in several banks which will store energy from single-frequency signals, which should be previously demodulated and parsed by frequency, of course. Also, the receiving module can be implemented as antenna field, or system with more antennas, placed in some pre-calculated and optimized space constellation in that way that the received energy would be the maximum possible for the current system.

The real prototype of the circuit

 

Picture 5: The real prototype of the circuit for utilization of the radio waves energy


As we mention above, we have implemented one real prototype of this circuit, for testing and experiment purposes. The real prototype is shown on Picture 5. On this prototype circuit we have connected two antennas, removed from an old wi-fi repeater. The rest of the circuit elements are same as the circuit we simulated (Picture 1). Before connecting the antennas on the circuit, which is actually how this circuit is put in operation, we made sure that the energy storing electrolytic capacitors C3 and C4 are totally discharged. After putting the circuit in operation, next day the measured voltage of its output was 273 mV, as shown on Picture 6.

Picture 6: Measuring the output voltage of the real prototype (after 1 day of accumulation)

Maxwell's Equations

Maxwell’s Equations provide a general description of electromagnetic phenomena. They are named after James Clerk Maxwell, the Scottish physicist whose pioneering work unified the theories of electricity and magnetism. The theory of electromagnetism was built on the discoveries and advances of many scientists and engineers, but the pivotal contribution was that of Maxwell.

The properties of the microscopic electro-magnetic (EM) field for stationary environments are expressed with well known system of Maxwell's equations, as shown on Picture 1:

Picture 1: System of Maxwell's Equations (for stationary environments)


I. The first equation is derived in compliance of the Ampere's Law with the law of continuation.
II. The second equation is a generalized form of Faraday's Law for electromagnetic induction.
III. The third equation expresses the generalized form of the Gauss theorem.
IV. The fourth equation represents the Law of conservation of magnetic flux.


When solving concrete systems, the Maxwell's Equations system need to be upgraded or supplemented with the following equations (Picture 2):

Picture 2: Additional equations for general Maxwell's Equations System


Here, the equation (1) represents the generalized form of the Ohm's Law, while with the equations (2) are expressed the vectors of electric displacement and magnetic induction. For linear and isotropic environments, these equations (2), are expressed in the form as represented with the equations (3).

The physical quantities included in all these equations above, are:

E - Electric field;
H - Magnetic field;
D - Electric displacement;
B - Magnetic induction;
J - Electric current density;
ρ - Distribution of electric charge;
σ - Specific electric conductance;
P - Electric polarization vector;
M - Vector of magnetization;
ε - Electric constant;
μ - Magnetic constant;

Blocking Oscillator with high/low Pulse/Pause periods

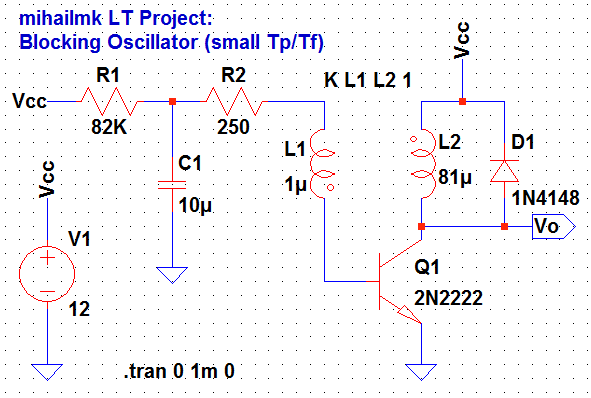
For purpose of generating signals with high or small pulse/pause relationship, the blocking oscillator with two accumulation elements is suitable circuit, as shown on Picture 1. The additional accumulation element in this circuit is the capacitor C1. Furthermore, at this blocking oscillator, the frequency of generated pulses can be changed, since the period when the transistor is blocked depends on the time constant R1*C1. So, changing the values of these elements, will change the frequency of the generated pulses.

Picture 1: Blocking Oscillator circuit with two accumulation elements

Time-domain analysis

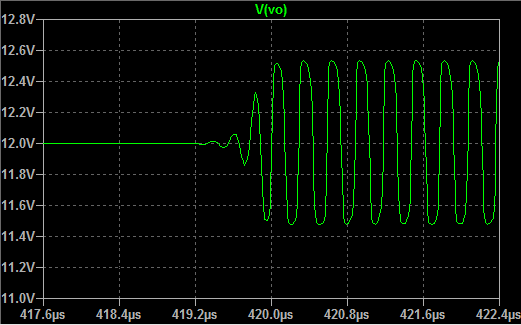
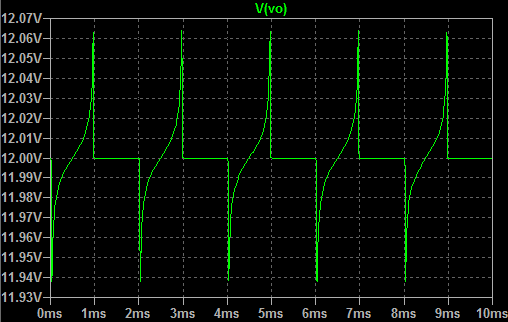
The results of the transient analysis for this circuit in time domain are shown on Picture 2. The output voltage Vo have low level periods of about 1.5 us when the voltage is about 123 mV, while the high level periods have duration of around 35.8 us and voltage values starts from 13 V and it's slowly falling to the value of 12.6 V. So, according to these results, the relationship between the periods of pulse and pause in output voltage is Tp/Tf = 35.8/1.5 = 23.86, which means is high.

Picture 2: Transient analysis - output voltage Vo wave form (time-domain)


Now, if we remove the diode D from the circuit, we will get the response which has small pulse/pause relationship. The wave form of this output voltage is shown on Picture 3. The time duration between the short pulses of the output voltage is around 4.61 us. After each high and short positive pulse, there is one short negative pulse of about -66 V, and after about 1.5 us the voltage cross the zero and goes into positive region with values around 4 mV and rising up to 450 mV at time region of 0.1 us before the next high peak. It's very interesting to notice here, that the positive peaks are to short in time, but extremely large in magnitude. As we can see from the plot on Picture 3, the starting peaks reach the voltage of around 4 KV (4000 V), which is very high and dangerous level. The time period when the peak voltage reaches values above 500 V is around 20 ns. So, if we chose this value as pulse period, then the relationship of pulse/pause for this circuit will be Tp/Tf = 0.02/4.61 = 0.004, and that's the desired very small value. However, this specific circuit generates these extremely high peaks just for the relatively short period of time. Namely, the peaks starts at values of around 4 KV and they decrease permanently, so after 5.56 ms the maximum values of the peaks falls below 50 V. At the time moment of 5.57 ms the circuit stops generating the extremely high voltage variations and oscillates around 12 V with magnitudes of around +/- 20 mV. So, this time region of extremely high voltage peaks it's kind of a transitional mode at the start of circuits work.

Picture 3: Transient analysis - output voltage Vo wave form without diode D (time-domain)

Astable Blocking Oscillator

With small variations of the Monostable Blocking Oscillator circuit, it can be provided to work into astable mode. The astable blocking oscillator circuit is shown on Picture 1. Its circuit is very simple and it consists of pulse transformer, diode, transistor and emitter resistor. The base of the transistor is positively polarized with the source Vbb, via the transformer coil L1. The source Vbb provides entry for the transistor into its saturation without external triggering pulse, thus in some period of time it generates similar wave form of the collector voltage as the monostable blocking oscillator.

Picture 1: Astable Blocking Oscillator circuit


After the period of saturation, when the transistor enters into active mode of operation with tendency of blocking, the voltage of the collector becomes Vc = Vcc + Vd, where Vd is the voltage threshold conduction of the diode D. Because the diode is conducting, it decreases the accumulated energy in the transformer coil L2, until the moment when the current of magnetization that flows through the L2 passes through zero changing its direction or polarization. At that moment, the diode becomes blocked, but the transistor is conducting starting with the new cycle of working mode.

Time-domain analysis

The results of the transient analysis for this circuit in time domain is shown on Picture 2. The output voltage Vo starts oscillating at about 383 us. The maximal peaks of the voltage are 12.53 V and the minimal peaks are 11.47 V, so the amplitude of oscillating voltage component is 53 mV. The period of oscillation or the time between two positive peaks is around 0.3 us, which corresponds to frequency of 3.33 MHz.

Picture 2: Transient analysis - output voltage Vo wave form (time-domain)

Blocking Oscillator (Monostable)

Blocking oscillator is a one-step relaxation generator with strong positive feedback, which is inductive and implemented with pulse transformer. The pulse transformer is the basic accumulation element of the assembly, and it has high inductance of magnetization of the primary coil, low leakage inductance, or low capacitance of the coils.

Since the pulse transformer is constructed with coefficient of coupling:

K = M/sqrt(Lp*Ls)

with value near to 1, where M is inter-inductance or mutual inductunce, Lp is primary inductance and Ls is secondary inductance. The transfer ratio of the transformer is defined as:

n = Vs/Vp = Ip/Is = Ns/Np = sqrt(Ls)/sqrt(Lp)

Here, the Ns and Np are the numbers of turns in secondary and primary coils, respectively. Vs, Vp and Is, Ip are the voltages and currents in the secondary and primary coils.

The blocking oscillator may generate short-time pulses with high frequency and high available power. Because of the strong positive feedback, the slope edge of the pulses is exceptionally high, while with application of third coil in the transformer it can be provided a generating of pulses with different amplitude and polarity. Depending on the set point for the DC mode of the active element, the blocking oscillator can work as monostable or astable assembly.

Picture 1: Monostable Blocking Oscillator circuit


On Picture 1 is shown an blocking oscillator in monostable mode provided with the negative voltage source applied to the base of the transistor and which the transistor in the blocking region, but because of the non-zero conduction threshold of the transistor, it takes that Vbb = 0, i.e. the base resistor can be connected to the ground. The activating of the transistor can be done if positive rise of its base voltage is provided. In our circuit, that's done with additional triggering transistor Q2, when it is lead to saturation which generates positive rise of the voltage in the base coil of the pulse transformer, L1.

We have to mention here, that the transformer element in LT spice can be configured as two, or more inductors depending of the number of coils of the transformer, and in order to specify the mutual inductunce by which actually we couple the inductors to act as a transformer, we need to insert a spice directive into our circuit in LT Spice with letter "K". After the letter K, we specify the coils that form the transformer and at the end we specify the mutual coupling coefficient, which value can goes from 0 to 1, where 1 means perfect coupling or in other words, no leakage inductance. Since we are simulating the circuit, the perfect coupling for the transformer we use would be just fine, so the spice directive for the model of the pulse transformer that we need to simulate in our circuit, as is shown on Picture 1, would be: "K L1 L2 1".

When the transistor Q1 exits the saturation mode, the accumulated charge in its base results in negative rise of the base current, while the accumulated energy of magnetization of the transformer coil L2 leads to positive rise of the collector voltage. In order to decrease these effects, the diode D is connected on the transformer coil L2.

Time-domain analysis

The results of the transient analysis for this circuit in time domain are shown on Picture 2 and Picture 3. The triggering signal applied to this circuit, VT is configured as sinusoidal signal with amplitude of 10 V at frequency of 500 Hz.

A. Transient analysis I

For this analysis, we use the negative or zero voltage for the voltage source Vbb. In our case, we set the Vbb = -5 V, but the same result can be achieved in case when Vbb = 0 V. So, with negative Vbb voltage, the output voltage of the circuit has slow and small oscillations, as shown on Picture 2. The output voltage varies around the 12 V with relative peaks of about +/- 60 mV. The time duration between two positive peaks is about 2 ms, which is corresponding to the frequency of 500 Hz, and that's exactly the frequency of the triggering signal.

Picture 2: Transient analysis I - output voltage Vo wave form (time-domain)

B. Transient analysis II

In this second analysis, we use the positive voltage for the voltage source Vbb, and in this case we set it to Vbb = +10 V. As it can be seen from Picture 3, the output voltage has periods of non-oscillating and oscillating states. Starting with non-oscillating state it changes between these states each milisecond, so it has stable value around 12 V for 1 ms, then starts oscillating between 14 and 1 V values for the next 1 ms, and so on. The zoom in of the wave form of Vo, is shown on Picture 4, where the oscillations of the voltage are noticeable.

Picture 3: Transient analysis II - output voltage Vo wave form (time-domain)


The high level of the output voltage starts with peak of about 14 V, then falls to about 12.75 V just before it enters the short negative peak of its low level, which is at around 1 V. The time duration between two peaks of the output voltage is about 1.3 us which corresponds to the frequency of about 769 kHz, and that's 1538 times greater frequency than the initial frequency of 500 Hz of the triggering pulse VT. This way, the monostable blocking oscillator circuit can be used to produce pulses with different frequency, in our case much higher than the frequency of the triggering voltage.

Picture 4: Transient analysis II - Zoom In of output voltage Vo wave form (time-domain)

Astable circuit with 555 Timer

The astable circuit with timer 555 is shown on Picture 1. In order to avoid the unwanted modulation during the controlling, the controlling pin of the circuit (CV-pin) is grounded via the capacitor C1 of 10 nF. The astable mode of work can be stopped with connecting the RST (reset) pin on low potential, and then, in order to reestablish the astable mode, the RST pin should be connected on high potential again.

Picture 1: Astable circuit with integrated 555 timer

Time-domain analysis

The results of the transient analysis for this circuit in time domain is shown on Picture 2. The output of the circuit is on its low level of about 7 mV, and the output high level of about 12 V. The first output pulse starts at about 1.1 ms and ends at about 2.5 ms, so the time duration of the output pulses is about 1.4 ms. The pause between the output pulses, when the output signal is at its low level, is about 0.7 ms.

Picture 2: Transient analysis - output voltage Vo wave form (time-domain)

Monostable circuit with 555 Timer

The integrated timer 555 is timer circuit intended for generating a rectangular pulses with voltage controlled time duration. The timer 555 can work in astable and monostable mode. The monostable circuit with timer 555 is shown on Picture 1. In order to avoid the unwanted modulation during the controlling, the controlling pin of the circuit (CV-pin) is grounded via the capacitor C3 of 10 nF.

Picture 1: Monostable circuit with integrated 555 timer

Time-domain analysis

The results of the transient analysis for this circuit in time domain is shown on Picture 2. On same picture are plotted both wave forms of the output Vo (green line plot) and the triggering voltage VT (blue line plot). As trigger voltage signal, here we use 3 rectangular pulses with amplitude of 5 V and time duration of about 50 ms, where the pause time between pulses or the duration of no trigger signal is about 150 ms. When the trigger signal is on high level (5 V), the output of the circuit is on its low level of about 4 mV, and the output high level is generated right after the input pulse. As it can be seen from the plot, when the input signal fails near the zero volts, the output starts increasing very fast to its high level of about 12 V. The first output pulse starts at about 60 ms and ends at about 81 ms, so the time duration of the output pulses is about 21 ms, and it can be varied by changing the values of the capacitor C1, through which the triggering pulse is leaded to the 555 timer circuit.

Picture 2: Transient analysis - output voltage Vo and trigger voltage VT wave forms (time-domain)

Monostable Multivibrator

Monostable multivibrator is an regenerative assembly which has one stable and one quasi-stable state. In other words, this is relaxation oscillator which when is activated (triggered) it generates one pulse on its output, and it stays blocked until the next trigger pulse is applied on its trigger input. The monostable multivibrator circuit is shown on Picture 1.

In the stable state the transistor Q2 is conducting (in saturation), thus the transistor Q1 is blocked, since the voltage divider R2/R6 provides the base voltage of Q1 to be on lower potential than its emitter. The emitter voltage is determined with the emitter current of the conducting transistor Q2. The assembly can be lead to unstable (quasi-stable) state or state of generating one pulse on its output Vo with applying of positive triggering pulse via the capacitor C2. Since in the stable state, the capacitor C1 is charged approximately to the value of Vcc - Ve, where Ve is the emitter voltage, with activating of the transistor Q1, the negative voltage of C1 is blocking the transistor Q2. The collector voltage of the Q2 increases, thus supporting the conduction of the Q1 in the transitional process until it gets into saturation and without further presence of the triggering pulse. The duration of the quasi-stable state is determined with the moment when the conditions for conducting of Q2 are again created by discharging of the capacitor C1 via the R3 and the conducting Q1.

So, it can be concluded that the successively triggering of the assembly, while it's already in the quasi-stable state, will take no effect. The duration of the quasi-stable mode can be approximately determined by the time constant defined with R3C1, multiplied by some real factor.

Picture 1: Monostable Multivibrator

Time-domain analysis

The results of the transient analysis for this circuit in time domain is shown on Picture 2. On same picture are plotted both wave forms of the output Vo (green line plot) and the triggering voltage VT (blue line plot). As trigger voltage signal, here we use 3 rectangular pulses with amplitude of 5 V and time duration of about 50 ms, where the pause time between pulses or the duration of no trigger signal is about 150 ms. When the trigger signal is on high level (5 V), the output of the circuit is on its high level of about 11 V, while the output low level, during the period when trigger signal is equal to zero, is about 150 mV.

Picture 2: Transient analysis - output voltage Vo and trigger voltage VT wave forms (time-domain)

Astable Multivibrator

Astable multivibrator is an assembly which has two quasi-stable states in which it goes through during the transitional mode. The simple circuit of astable multivibrator is shown on Picture 1. It contains two amplifiers connected in common emitter connection which works as inverters. Also, a strong positive feedback is implemented from the collector of the one transistor to the base of the other, and vice versa. As it can be expected for the system with positive feedback, the assembly has regenerative properties if the circularly amplification is higher than 1, which can be achieved if the values for the base and collector resistors are selected to satisfy: R2/R1 < hfe - parameter of the selected transistor. The frequency of oscillation will be determined with the base resistors R2, R3 and with capacitors C1, C2. Because the transistors alternately goes from mode of saturation into blocking mode, the wave form of the voltage on their collectors it's basically rectangular, so the outputs V1 and V2 are complimentary, or phase-shifted for 180 degrees.  

Picture 1: Astable Multivibrator


At the astable multivibrators where the base current of the transistors is far more higher than the current needed for their saturation, it may occur the state where the assembly is blocked if both transistors are in saturation at same time. In order to prevent this kind of blocking of the assembly, the saturation factor of the transistors should be decreased by increasing the values of resistance of the base resistors R2 and R3, or by decreasing the values of collector resistors R1 and R4. As can be seen from Picture 1, the values of R1 = R4 = 1K, and R2 = R3 = 28K ohms.

Time-domain analysis

The results of the transient analysis for this circuit in time domain is shown on Picture 2. On same picture are plotted both wave forms of the outputs V1 (green line plot) and V2 (blue line plot). The high level of the outputs is about 12 V, while the low level is near to zero or about 54 mV, which is actually the saturation voltage Vce(sat) of the transistors BC547C for this circuit configuration, the models used in this simulation. The duration of high/low levels is about 0.5 ms, and this value can be altered with different values for the capacitors C1 and C2, and the base resistors R2 and R3.

Picture 2: Transient analysis - output voltage V1 and V2 wave forms (time-domain)

Linduino

Linduino is Linear Technology’s Arduino compatible system for developing and distributing firmware libraries and example code for Linear Technology’s integrated circuits. The code is designed to be highly portable to other microcontroller platforms, and is written in C using as few processor specific functions as possible. The code libraries can be downloaded by clicking the Downloads tab above and used as-is in your project or individual code snippets may be viewed in the Code section of a supported part. The Linduino One board (Demonstration Circuit DC2026) allows you to test out the code directly, using the standard demo board for the particular IC.

The Linduino One board is compatible with the Arduino Uno, using the Atmel ATMEGA328 processor. This board features a 14-pin “QuikEval” connector that can be plugged into nearly 100 daughter boards for various Linear Technology parts, including Analog to Digital converters, Digital to Analog Converters, high-voltage power monitors, temperature measurement devices, RF synthesizers, battery stack monitors, and more.

An LTM2884 USB Isolator breaks the ground connection to the PC, allowing projects to operate at a different ground potential than the computer that is controlling it.

Linduino is Linear Technology’s Arduino compatible development platform. Linduino is a package; it is a complete solution. Linduino has a board, the Linduino One. The Linduino One is a Arduino Uno compatible development board, with a twist, it comes with a LTM2884 uModule that provides full USB isolation. Even more importantly the board also comes with a 14 pin QuikEval connector that allows the Linduino One to directly connect to hundreds of LTC QuickEval compatible demo boards, already in existence.

However, the board is only part of Linduino. The real meat of Linduino is not the demo board but the library of example firmware that comes backing the One. The main goal of the Linduino program is to provide customers with example firmware to help them interact with Linear Tech’s parts. The Linduino One is merely there to provide a consistent development platform for the end customer. This library of code is intended to compile in any standard C compiler, we have taken steps to try to make the examples as portable as possible. As a matter of fact, the code is fully Arduino compatible, so if you have a spare Arduino Uno and the will to solder a couple of connections, you’re already ready to play. The goal of this entire package of goodies that we’ve built is to save time.

The idea is that a hardware engineer trying to interface a 24 bit ADC such as the LTC2449 into his circuit is a couple clicks away from loading the running, tested code into a microcontroller and talking to the part. Once the engineer is done with their testing, the example code snippets that were used can be ported over to the processor they are using for their end product. This should greatly shorten their development time.


More information and free download available here: Linduino.


Source: Linear Technology.

Bistable Multivibrator (Trigger circuit)

The switching electronic assemblies contains elements that are working in switching mode and they can be of non-regenerative or regenerative type. At the non-regenerative assemblies the state of the output is a function of the input signal only, while at the regenerative assemblies the state of the output doesn't depend only on the input signal, but also it depends on the previous state of the assembly. The regenerative assemblies are mostly implemented as two-step amplifiers with strong positive feedback, which allows fast changing of the states of the active amplifiers between the mode of conduction into the mode of stopping or saturation.

Depending on the configuration, the regenerative assemblies can have two stable states, one stable and one quasi-stable (transitional) state or two quasi-stable states.

Bistable multivibrator

Bistable multivibrator (trigger, flip-flop), is a regenerative assembly with two stable states, where the transition from one into another state is performed with step-change under the influence of the trigger (control) signal. The controlling of the trigger can be done with applying short pulses on the transistors bases. If the triggering pulses are generated from one source, then the controlling is called symmetric triggering, and if are used two independent sources, then it's called non-symmetric triggering. In case of non-symmetric triggering, one of the inputs serves as set input for setting the trigger in state Q = 1, and the other input serves as reset input for its deletion, Q = 0.

The trigger circuit shown on Picture 1 is a bistable multivibrator which consists two amplifiers with bipolar transistors (inverters). The two outputs of this circuits are marked as V1 and V2. The output of each inverter serves as a input for the other. In one stable state of the assembly, the transistor Q1 is in saturation, while the transistor Q2 is blocked. For this state, the output V2 is on some positive potential level and the output V1 is near to zero, which is the saturation voltage between the collector and emitter of Q1. In the other stable state Q1 is blocked and Q2 is in saturation, so the output V1 is on some positive level and V2 is near to zero.

Picture 1: Bistable Multivibrator


The speed of the trigger, or the duration of the transition mode which starts with applying of the triggering pulses, in general it depends on the switching parameters of the transistors. So, for the transistors with higher current amplification and lower time constant of its base, which are actually a high-frequency transistors, the speed of the trigger would be higher. The higher speeds of work can also be achieved with lower values of the resistors R1 and R2, but in that case the dissipation of the trigger is increased. However, the regenerative process can be speed up without increasing the dissipation of the trigger, and that's done in our circuit with the capacitors C1 and C2. Adding the capacitors, shunts the resistors R2 and R5 in the transitional mode, so the step changes in the collector are reflected in the base of the other transistor which provides faster commutation or switching of the trigger.

Time-domain analysis

The values of the resistors R1 and R4 are usually equal, which means the trigger is symmetric, and those values are selected for the wanted collector current of saturation. If the resistor values satisfy R2 = R5 = 10*R1 and R3 = R6 = 3*R2, as it is in the case of the circuit on Picture 1, then the reliable operation of the trigger is provided with current amplification factor of 20, which is common feature of any standard bipolar transistor.

It can be noticed that the functionality of the trigger will not be broken if the resistors R3 and R6 are removed, since it would still be satisfied that Vbe > Vce, but in that case it should be provided deeper permeation of the transistors in their region of saturation. In our circuit we choose the power supply voltages of Vcc = Vbb = 12 V.

Picture 2: Transient analysis - output voltage V1 and V2 wave forms (time-domain)


The results of the transient analysis for this circuit in time domain is shown on Picture 2. On same picture are plotted both wave forms of the outputs V1 (green line plot) and V2 (blue line plot). The high level of the outputs is about 11 V, while the low level is near to zero or about 17 mV, which is actually the saturation voltage Vce(sat) of the transistors BC547C, the models used in this simulation. The duration of high/low levels is about 1.5 ms, and this value can be altered with different values for the capacitors C1 and C2.

Linear Shaping of Signals | RC(LR) & CR(RL) circuits

When simple periodic (sinusoidal) signals are applied on the electric circuits which contains linear R, L, C elements, then the response of these circuits in stationary mode is proportional to the input signal. The effect of these circuits on the input signal is expressed only with the relationship of the amplitudes or the phases of the input and output signal, but the shape of the signal is preserved. Therefore, these kind of circuits are called linear electric circuits. However, the response of these circuits for complex, not-simple periodic signal, will undergo change not only in the amplitude of the signal, but also in its shape, due to the unequal impact of the circuits on the harmonic components contained in the input signal. The process of changing the shape of the signals through these kind of linear circuits is called linear shaping of signals.

In the pulse electronics, the not-simple periodic signals are exactly of great importance. These signals are so called pulse signals and they are characterized with step change in their amplitude. Examples of pulse signals are: rectangular pulses, linear increasing/decreasing signals, exponentional signals, aperiodic pulse signals with complex shape, and so on.

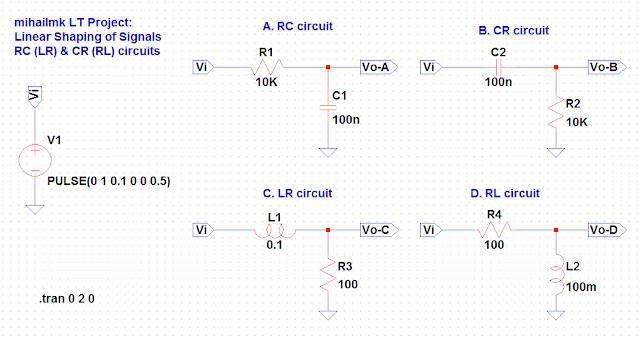
Picture 1: Simple RC(LR) & CR(RL) circuits for Linear Shaping of Signals


On Picture 1 are shown simple examples of RC(LR) and CR(RL) circuits. Because of the way of which these circuits impact on the harmonics from the spectrum of the input signal, they are called low-pass or high-pass circuits. According to the function of these circuits, the circuit A. (RC circuit) is equivalent to the circuit C. (LR circuit) and the circuit B. (CR circuit) is equivalent to the circuit D. (RL circuit), if the relation RC = L/R is satisfied.

The analysis of these circuits is based on the energy state of the energy storage elements, capacitor C and inductor L, that can be expressed via the dynamic equations which describes the physical nature of these elements. In other words, the voltage of the capacitor ends through which flows final current, can not have an discontinuous change, or it must apply that Vc(t+) = Vc(t-). The current that flows through inductor coil which is exposed on the final voltage on its ends, can not have an step change, or it must apply that iL(t+) = iL(t-).

If a step-voltage is applied on the input of linear RC circuit, then the response of the circuit will follow some shape from starting value to final value of the output signal. In theory, the final value of the output voltage will be achieved after infinitely long time. However, in practice, the 95% of the final value is achieved after the period of time t = 3τ, where τ = RC is the time constant of the circuit. This time is considered sufficient for achieving the stationary (steady) state of the circuit.

In many applications of great importance is the time duration of the front, or rear edge of the signal, the so called rise-time, or fall-time, which is defined as time needed for change in the amplitude of the signal from 10% up to 90% of its final value.

Time-domain analysis

Now, let's see the results of the transient analysis for these 4 linear circuits in time domain. We choose to analyze the response of these circuits for the rectangular pulse as input signal. Therefore, we set the independent voltage source V1 as pulse generator, to generate the rectangular pulse with amplitude of 1 V and time duration of 0.5 seconds. The delay time period for this pulse is set to 100 ms, and the rise-time and fall-time are set to zero. The input voltage wave form is shown on Picture 2. Although we set the rise and fall time of the pulse to zero, as we can see from the plot, it takes of about 50 ms for the pulse to achieve the value of 1 V and fall back to zero volts again.

Picture 2: Input voltage wave form (time-domain)


Furthermore, as we can see from the circuit elements shown on Picture 1, we chose the values of 100 nF and 10 kOhms for the CR and RC circuits, so their time constant is equal to τ = RC = 1 ms. Also, for the LR and RL circuits we choose values of 100 mH and 100 ohms, so their time constant is also τ = L/R = 1 ms. Thus, we have satisfied the condition RC = L/R, so the A. and C. circuits are equivalent, and B. and D. circuits are also equivalent.

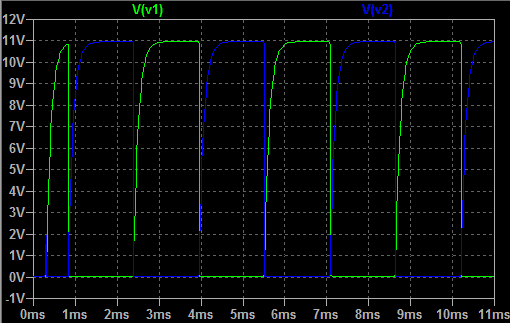
Picture 3: Output voltage wave forms of the A. RC circuit & C. LR circuit (time-domain)


The wave forms of the output voltages Vo-A and Vo-C are shown on Picture 3. As we can see, both plots match to eachother as expected from the condition of equal time constants. Furthermore, they match the input voltage signal, so we can say that these two circuits A. and C. do not affect the input signal at all, since they didn't change its shape, nor it's amplitude.

Picture 4: Output voltage wave forms of the B. CR circuit & D. RL circuit (time-domain)


From the other hand, the circuits B. and D. have changed the shape of the input signal, as we can see from Picture 4. The wave forms of the output voltages Vo-B and Vo-D are both same, as expected. We can notice that these ouput signals consists of two rectangular pulses. The first of them is positive with amplitude of +20 mV and time duration of about 50 ms, which match the timing of rising of the input signal, and the second pulse is negative with amplitude of -20 mV and same duration of about 50 ms, which match the timing of falling of the input signal from 1 to 0 volts.

Square Wave Generator

This circuit (shown on Picture 1) is an oscillator that generates a square wave. It is also known as an astable multivibrator. The op amp works as a comparator. Let’s assume that the op amp output goes high on power on, thus making Vo = +Vz, where Vz is the breakdown voltage of the zener diode. The capacitor charges with a time constant τ = R4C1. When the capacitor voltage reaches βVo, where β = R2/(R1 + R2), the op amp output switches low, and Vo = −Vz, as shown in the graph on Picture 2.

Picture 1: Square Wave Generator circuit


The zener diodes used in this circuit, as shown on Picture 1, are of type EDZV6_2B with breakdown voltage of 6.2 V. The time constant with which the capacitor C1 charges is equal to τ = R4C1 = 1 ms. The value of beta factor for this circuit is β = R2/(R1 + R2) = 1/2, so, the capacitor voltage should reach half of the output voltage.

Picture 2: The output and capacitor voltages


Time-domain analysis

The results of the transient analysis for this circuit in time domain, are shown on Picture 3. The output voltage starts to increase at about 33 ms. The first peak of the output voltage is about 4.51 V and it's reached at time of about 39.3 ms. After about 42 ms the output voltage continues to oscillate with period of about 2.65 ms, which means that the frequency of the oscillations is about 377 Hz. The maximum and minimum values of the Vo are about +/- 5.4 V. The voltage of the capacitor C1 oscillates with same frequency, with values between +/- 2.7 V. The voltage of the zener diode D2 varies from about + 4.9 V to about -500 mV, when the output voltage reaches it's negative peak.

Picture 3: Transient analysis - output voltage wave form (time-domain)

Phase-shift Oscillator

The circuit shown on the Picture 1 is phase-shift oscillator. The conditions for this circuit to start the oscillations are R1 = R2 = R3 = R and C1 = C2 = C3 = C and the feedback resistor is Rfb = 29R. The frequency of the oscillations and the conditions are defined with the formulas shown on Picture 2.

Picture 1: Phase-shift Oscillator circuit

Picture 2: Frequency of oscillations for phase-shift oscillator circuit

Wien bridge Oscillator

The circuit shown on the Picture 1 is Wien bridge oscillator. The resistor Rb is actually the resistance of the bulb which is self-heating up to the point when Rb = Rf/2. Another condition for this circuit to start the oscillations is R1 = R2 = R and C1 = C2 = C. The frequency of the oscillations and the conditions are defined with the formulas shown on Picture 2.

Picture 1: Wien bridge Oscillator circuit

Picture 2: Frequency of oscillations for Wien bridge oscillator circuit

Hartley Oscillator

The circuit shown on Picture 1 is Hartley oscillator in its op-amp version. The frequency of the generated oscillations from this circuit is defined by the formulas shown on Picture 2. The inductance coils L1 and L2 can be magnetically coupled or not, thus affecting the resulting inductance L which directly affect the frequency of oscillations of this circuit.

Picture 1: Hartley Oscillator circuit

Picture 2: Frequency of oscillations for Hartley oscillator circuit

Pentode Tube Amplifier

The pentode vacuum tube amplifier circuit configuration is shown on Picture 1. The pentode tube used in this circuit is the EL84 or 6BQ5 tube spice model. The heater circuit for the cathode is not shown in this symbol, but it's on 6.3 V AC or DC voltage and it consumes current of 760 mA. The power supply voltage for this circuit is Us = 450 V DC. This voltage is leaded to the anode of the pentode tube through the resistor Ra = 82 kOhms and to the screen electrode or grid 3 through the resistor Rs = 220 kOhms. The cathode is connected to the ground through the parallel combination of the resistor Rk = 2.2 kOhms and the electrolytic capacitor C3 = 270 uF. For the proper polarization of the grid 1 the resistors Rm = 1 MOhms and Rg = 10 kOhms take places. The input voltage signal is leaded to the grid of the pentode through the capacitor C1 and the resistor Rg. The output voltage is taken from the anode of the pentode through the capacitor C2 and is leaded to the load resistor Rload = 10 kOhms. The both coupling capacitors are C1 = C2 = 1 uF.

Picture 1: Pentode Tube Amplifier Circuit


Time-domain analysis

The results of the transient analysis in time domain for this circuit are shown on Picture 2. The green color line plot is the output voltage wave form and the blue color line plot is the input voltage wave form. Since the pentode tube is more powerful than the triode tube, we can consider that this circuit can be driven by the triode tube stage, so, as output power stage it can be excited with higher voltage level. In this case, the input voltage source is with sinusoidal waveform with amplitude of 1 V at frequency of 1 kHz. The output varies from about +/- 5.9 V amplitudes, it is phase inverted from the input. The voltage amplification of this circuit is about Av = 5.8, and the current amplification is about Ai = 584. These are the results from the simulation:

For Vi max = + 1 V => Vo min = - 6.02 V;
For Vi min = - 1 V => Vo max = + 5.85 V;

--> Av = 5.8 (approximate voltage amplification Av = Vo/Vi)

For Ic1 min = - 1 uA => IRl max = + 584 uA;
For IC1 max = + 1 uA => IRl min = - 602 uA;

--> Ai = 584 (approximate current amplification Ai = Io/Ii)

Picture 2: Transient analysis - input and output voltage wave forms (time-domain)



Frequency-domain analysis

The phase-frequency characteristics of this common cathode circuit were measured with AC analysis in LT spice. LT Spice computes the small signal AC behavior of the circuit linearized about its DC operating point. In this AC simulation were used these parameters:

Type of Sweep: Octave;
Number of points per octave: 1;
Start Frequency: 20 Hz;
Stop Frequency: 10 MHz;

Picture 3: AC Analysis - output voltage [dB] and its phase [degrees] (frequency-domain)


This circuit has a flat amplification for frequencies up to 1 MHz. The magnitude of the output voltage in this band is about + 15.5 dB. The magnitude decreases for 3 dB at frequency of 1.06 MHz with phase of -232.9 degrees and group delay of 100.4 ns. This is the high frequency limit for this circuit fH = 1.06 MHz. At frequency of 20 Hz the magnitude of the output voltage is 15 dB with phase of -159.4 degrees and group delay of 1.72 ms. At frequency of 10 MHz the magnitude of the output voltage is -8.8 dB with phase of -320.6 degrees and group delay of 4.9 ns. According to the results of the AC analysis this circuit has relatively flat voltage amplification for the audio signals and has no low frequency limit. The phase-frequency characteristics of the circuit is shown on the Picture 3.

Common Anode Triode Tube Amplifier

The common anode triode vacuum tube amplifier is is shown on Picture 1. The triode used in this circuit is the ECC83 tube, or 12AX7. The power supply for the circuit is Us = 250 V DC. The heater of the triode is not shown in the circuit, but is standard triode heater at 6.3 V AC or DC and one triode heater consumes 150 mA current. The power supply voltage is leaded directly to the anode of the triode. The cathode of the tube is connected to the ground through the resistor Rk = 4.7 Kohm, and here the electrolytic capacitor is removed in order to not affect the output signal which is taken from the cathode. For proper polarization of the grid the resistors Rm = 1 MOhms and Rg = 10 kOhms takes place. The amplified output signal is taken from the cathode of the tube through the coupling capacitor C2 and leaded to the load, resistor Rload = 5 kOhms. The coupling capacitors are both C1 = C2 = 1 uF. The input signal is leaded to the grid of the tube through the C1 and Rg.

Picture 1: Common Anode Triode Tube Amplifier Circuit


Time-domain analysis

The results of the transient analysis in time domain for this circuit are shown on Picture 2. The green color line plot is the output voltage wave form and the blue color line plot is the input voltage wave form. The input voltage source is with sinusoidal wave form with amplitude of 100 mV at frequency of 1 kHz. The output varies from about +/- 0.08 V amplitudes, it is in phase with the input. The voltage amplification of this circuit is about Av = 0.8, and the current amplification is about Ai = 158. Here, the voltage amplification is below 1. These are the results from the simulation:

For Vi max = + 100 mV => Vo max = + 78.84 mV;
For Vi min = - 100 mV => Vo min = - 79.16 mV;

--> Av = 0.8 (approximate voltage amplification Av = Vo/Vi)

For Ic1 min = - 99 nA => IRl min = - 15.8 uA;
For IC1 max = + 99 nA => IRl max = + 15.7 uA;

--> Ai = 158 (approximate current amplification Ai = Io/Ii)

Picture 2: Transient analysis - input and output voltage wave forms (time-domain)


Frequency-domain analysis

The phase-frequency characteristics of this common cathode circuit were measured with AC analysis in LT spice. LT Spice computes the small signal AC behavior of the circuit linearized about its DC operating point. In this AC simulation were used these parameters:

Type of Sweep: Octave;
Number of points per octave: 1;
Start Frequency: 20 Hz;
Stop Frequency: 10 MHz;

Picture 3: AC Analysis - output voltage [dB] and its phase [degrees] (frequency-domain)


This circuit has a flat amplification from frequency at about 500 Hz up to 1 MHz, as shown on Picture 3. The magnitude of the output voltage in this band is -22 dB. At frequency of 31 Hz the magnitude decreases for 3 dB at value of -25 dB with phase of 44.8 degrees and group delay of 2.6 us. So, the low frequency limit for this circuit is fL = 31 Hz. The magnitude decreases for 3 dB again at frequency of 8 MHz with phase of -44.2 degrees and group delay of 9.8 ns. This is the high frequency limit for this circuit fH = 8 MHz. At frequency of 20 Hz the magnitude of the output voltage is -26.8 dB with phase of 55.6 degrees and group delay of 3.27 us. At frequency of 10 MHz the magnitude of the output voltage is -26.2 dB with phase of -51.7 degrees and group delay of 6.8 ns. According to the results of the AC analysis this circuit has relatively flat voltage amplification for the audio signals. The voltage amplification is below 1, but it is near one, and similar like the common collector amplifier, this circuit acts like voltage follower, the output voltage simply follows the input voltage. From the other side, the circuit has a relatively big current amplification.

Common Grid Triode Tube Amplifier

The common grid triode vacuum tube amplifier is is shown on Picture 1. The triode used in this circuit is the ECC83 tube, or 12AX7. The power supply for the circuit is Us = 250 V DC. The heater of the triode is not shown in the circuit, but is standard triode heater at 6.3 V AC or DC and one triode heater consumes 150 mA current. The power supply voltage is leaded to the anode of the triode through the anode resistor Ra = 100 kOhms. The cathode of the tube is connected to the ground through the resistor Rk = 1 Kohm, and here the electrolytic capacitor is removed in order to not affect the input signal which is leaded to the cathode. For proper polarization of the grid the resistors Rm = 1 MOhms and Rg = 10 kOhms takes place. The amplified output signal is taken from the anode of the tube through the coupling capacitor C2 and leaded to the load, resistor Rload = 5 kOhms. The coupling capacitors are both C1 = C2 = 1 uF.

Picture 1: Common Grid Triode Tube Amplifier Circuit


Time-domain analysis

The results of the transient analysis in time domain for this circuit are shown on Picture 2. The green color line plot is the output voltage wave form and the blue color line plot is the input voltage wave form. The input voltage source is with sinusoidal wave form with amplitude of 100 mV at frequency of 1 kHz. The output varies from about +/- 0.8 V amplitudes, it is in phase with the input, but delayed for about 0.5 ms. The voltage amplification of this circuit is about Av = 8.5, and the current amplification is about Ai = 0.6. The current amplification is below 1. These are the results from the simulation:

For Vi max = + 100 mV => Vo max = + 827.23 mV;
For Vi min = - 100 mV => Vo min = - 858.75 mV;

--> Av = 8.5 (approximate voltage amplification Av = Vo/Vi)

For Ic1 min = - 272 uA => IRl min = - 177 uA;
For IC1 max = + 266 uA => IRl max = + 165 uA;

--> Ai = 0.6 (approximate current amplification Ai = Io/Ii)

Picture 2: Transient analysis - input and output voltage wave forms (time-domain)


Frequency-domain analysis

The phase-frequency characteristics of this common cathode circuit were measured with AC analysis in LT spice. LT Spice computes the small signal AC behavior of the circuit linearized about its DC operating point. In this AC simulation were used these parameters:

Type of Sweep: Octave;
Number of points per octave: 1;
Start Frequency: 20 Hz;
Stop Frequency: 10 MHz;

Picture 3: AC Analysis - output voltage [dB] and its phase [degrees] (frequency-domain)


The maximum voltage magnitude is about -1 dB at frequency of about 2.1 kHz with phase of 1.1 degrees, as shown on Picture 3. At frequency of 466 Hz the magnitude decreases at -4 dB with phase of 44.9 degrees and group delay of 194 us. So, the low frequency limit for this circuit is fL = 466 Hz. The magnitude decreases for 3 dB again at frequency of 9.2 kHz with phase of -38.7 degrees and group delay of 8.8 us. This is the high frequency limit for this circuit fH = 9.2 kHz. At frequency of 20 Hz the magnitude of the output voltage is -28.2 dB with phase of 94.4 degrees and group delay of 949.1 us. At frequency of 10 MHz the magnitude of output voltage is -21.5 dB with phase of 126.2 degrees and group delay of 38.9 ps. According to the results of the AC analysis this circuit has relatively small frequency band from low to high limit, which is less than 9 kHz.