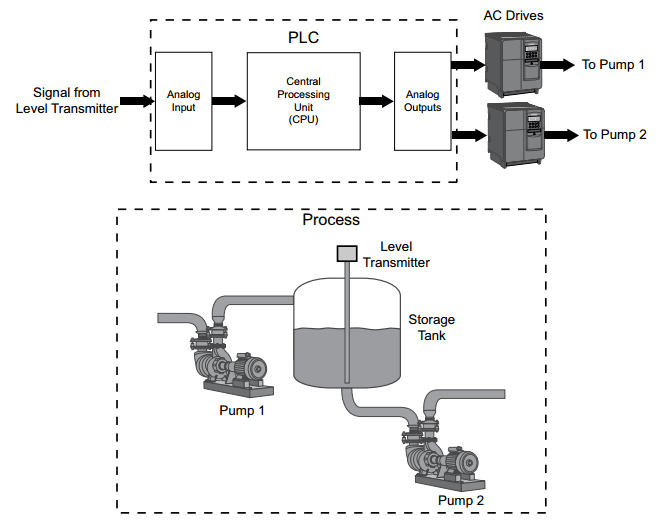
The definition of proper sampling is quite simple. Suppose you sample a continuous signal in some manner. If you can exactly reconstruct the analog signal from the samples, you must have done the sampling properly. Even if the sampled data appears confusing or incomplete, the key information has been captured if you can reverse the process.
Picture 1 shows several sinusoids before and after digitization. The continuous line represents the analog signal entering the ADC, while the square markers are the digital signal leaving the ADC. In
(a), the analog signal is a constant DC value, a cosine wave of zero frequency. Since the analog signal is a series of straight lines between each of the samples, all of the information needed to reconstruct the analog signal is contained in the digital data. According to our definition, this is proper sampling.
Picture 1: Illustration of proper and improper sampling
The sine wave shown in
(b) has a frequency of 0.09 of the sampling rate. This might represent, for example, a 90 cycle/second sine wave being sampled at 1000 samples/second. Expressed in another way, there are 11.1 samples taken over each complete cycle of the sinusoid. This situation is more complicated than the previous case, because the analog signal cannot be reconstructed by simply drawing straight lines between the data points. Do these samples properly represent the analog signal? The answer is yes, because no other sinusoid, or combination of sinusoids, will produce this pattern of samples (within the reasonable constraints listed below). These samples correspond to only one analog signal, and therefore the analog signal can be exactly reconstructed. Again, an instance of proper sampling.
In
(c), the situation is made more difficult by increasing the sine wave's frequency to 0.31 of the sampling rate. This results in only 3.2 samples per sine wave cycle. Here the samples are so sparse that they don't even appear to follow the general trend of the analog signal. Do these samples properly represent the analog waveform? Again, the answer is yes, and for exactly the same reason. The samples are a unique representation of the analog signal. All of the information needed to reconstruct the continuous waveform is contained in the digital data. How you go about doing this will be discussed later in this chapter. Obviously, it must be more sophisticated than just drawing straight lines between the data points. As strange as it seems, this is proper sampling according to our definition.
In
(d), the analog frequency is pushed even higher to 0.95 of the sampling rate, with a mere 1.05 samples per sine wave cycle. Do these samples properly represent the data? No, they don't! The samples represent a different sine wave from the one contained in the analog signal. In particular, the original sine wave of 0.95 frequency misrepresents itself as a sine wave of 0.05 frequency in the digital signal. This phenomenon of sinusoids changing frequency during sampling is called aliasing. Just as a criminal might take on an assumed name or identity (an alias), the sinusoid assumes another frequency that is not its own. Since the digital data is no longer uniquely related to a particular analog signal, an unambiguous reconstruction is impossible. There is nothing in the sampled data to suggest that the original analog signal had a frequency of 0.95 rather than 0.05. The sine wave has hidden its true identity completely; the perfect crime has been committed! According to our definition, this is an example of improper sampling.
This line of reasoning leads to a milestone in DSP, the sampling theorem. Frequently this is called the
Shannon sampling theorem, or the
Nyquist sampling theorem, after the authors of 1940s papers on the topic. The sampling theorem indicates that a continuous signal can be properly sampled, only if it does not contain frequency components above one-half of the sampling rate. For instance, a sampling rate of 2,000 samples/second requires the analog signal to be composed of frequencies below 1000 cycles/second. If frequencies above this limit are present in the signal, they will be aliased to frequencies between 0 and 1000 cycles/second, combining with whatever information that was legitimately there.
Two terms are widely used when discussing the sampling theorem: the Nyquist frequency and the Nyquist rate. Unfortunately, their meaning is not standardized. To understand this, consider an analog signal composed of frequencies between DC and 3 kHz. To properly digitize this signal it must be sampled at 6,000 samples/sec (6 kHz) or higher. Suppose we choose to sample at 8,000 samples/sec (8 kHz), allowing frequencies between DC and 4 kHz to be properly represented. In this situation there are four important frequencies: (1) the highest frequency in the signal, 3 kHz; (2) twice this frequency, 6 kHz; (3) the sampling rate, 8 kHz; and (4) one-half the sampling rate, 4 kHz. Which of these four is the Nyquist frequency and which is the Nyquist rate? It depends who you ask! All of the possible combinations are used. Fortunately, most authors are careful to define how they are using the terms. Here, they are both used to mean one-half the sampling rate.
Picture 2 shows how frequencies are changed during aliasing. The key point to remember is that a digital signal cannot contain frequencies above one-half the sampling rate (i.e., the Nyquist frequency/rate). When the frequency of the continuous wave is below the Nyquist rate, the frequency of the sampled data is a match. However, when the continuous signal's frequency is above the Nyquist rate, aliasing changes the frequency into something that can be represented in the sampled data. As shown by the zigzagging line in
Picture 2, every continuous frequency above the Nyquist rate has a corresponding digital frequency between zero and one-half the sampling rate. If there happens to be a sinusoid already at this lower frequency, the aliased signal will add to it, resulting in a loss of information. Aliasing is a double curse; information can be lost about the higher and the lower frequency. Suppose you are given a digital signal containing a frequency of 0.2 of the sampling rate. If this signal were obtained by proper sampling, the original analog signal must have had a frequency of 0.2. If aliasing took place during sampling, the digital frequency of 0.2 could have come from any one of an infinite number of frequencies in the analog signal: 0.2, 0.8, 1.2, 1.8, 2.2, ... .
Picture 2: Conversion of analog frequency into digital frequency during sampling
Just as aliasing can change the frequency during sampling, it can also change the phase. For example, look back at the aliased signal in
Picture 1 (d). The aliased digital signal is inverted from the original analog signal; one is a sine wave while the other is a negative sine wave. In other words, aliasing has changed the frequency and introduced a 180E phase shift. Only two phase shifts are possible: 0E (no phase shift) and 180E (inversion). The zero phase shift occurs for analog frequencies of 0 to 0.5, 1.0 to 1.5, 2.0 to 2.5, etc. An inverted phase occurs for analog frequencies of 0.5 to 1.0, 1.5 to 2.0, 2.5 to 3.0, and so on.
Now we will dive into a more detailed analysis of sampling and how aliasing occurs. Our overall goal is to understand what happens to the information when a signal is converted from a continuous to a discrete form. The problem is, these are very different things; one is a continuous waveform while the other is an array of numbers. This "apples-to-oranges" comparison makes the analysis very difficult. The solution is to introduce a theoretical concept called the impulse train.
Picture 3 (a) shows an example analog signal.
Picture 3 (c) shows the signal sampled by using an impulse train. The impulse train is a continuous signal consisting of a series of narrow spikes (impulses) that match the original signal at the sampling instants. Each impulse is infinitesimally narrow. Between these sampling times the value of the waveform is zero. Keep in mind that the impulse train is a theoretical concept, not a waveform that can exist in an electronic circuit. Since both the original analog signal and the impulse train are continuous wave forms, we can make an "apples-apples" comparison between the two.
Picture 3: The sampling theorem in the time and frequency domains
Now we need to examine the relationship between the impulse train and the discrete signal (an array of numbers). This one is easy; in terms of information content, they are identical. If one is known, it is trivial to calculate the other. Think of these as different ends of a bridge crossing between the analog and digital worlds. This means we have achieved our overall goal once we understand the consequences of changing the waveform in
Picture 3 (a) into the waveform in
Picture 3 (c).
Three continuous wave forms are shown in the left-hand column in
Picture 3. The corresponding frequency spectra of these signals are displayed in the right-hand column. This should be a familiar concept from your knowledge of electronics; every waveform can be viewed as being composed of sinusoids of varying amplitude and frequency. Later chapters will discuss the frequency domain in detail.
Picture 3 (a) shows an analog signal we wish to sample. As indicated by its frequency spectrum in
(b), it is composed only of frequency components between 0 and about 0.33 f
s, where f
s is the sampling frequency we intend to use. For example, this might be a speech signal that has been filtered to remove all frequencies above 3.3 kHz. Correspondingly, f
s would be 10 kHz (10,000 samples/second), our intended sampling rate.
Sampling the signal in
(a) by using an impulse train produces the signal shown in
(c), and its frequency spectrum shown in
(d). This spectrum is a duplication of the spectrum of the original signal. Each multiple of the sampling frequency, f
s, 2f
s, 3f
s, 4f
s, etc., has received a copy and a left-for-right flipped copy of the original frequency spectrum. The copy is called the upper side-band, while the flipped copy is called the lower side-band. Sampling has generated new frequencies. Is this proper sampling? The answer is yes, because the signal in
(c) can be transformed back into the signal in
(a) by eliminating all frequencies above ½fs. That is, an analog low-pass filter will convert the impulse train,
(b), back into the original analog signal,
(a).
If you are already familiar with the basics of DSP, here is a more technical explanation of why this spectral duplication occurs. In the time domain, sampling is achieved by multiplying the original signal by an impulse train of unity amplitude spikes. The frequency spectrum of this unity amplitude impulse train is also a unity amplitude impulse train, with the spikes occurring at multiples of the sampling frequency, f
s, 2f
s, 3f
s, 4f
s, etc. When two time domain signals are multiplied, their frequency spectra are convolved. This results in the original spectrum being duplicated to the location of each spike in the impulse train's spectrum. Viewing the original signal as composed of both positive and negative frequencies accounts for the upper and lower side-bands, respectively. This is the same as amplitude modulation.
Picture 3 (e) shows an example of improper sampling, resulting from too low of sampling rate. The analog signal still contains frequencies up to 3.3 kHz, but the sampling rate has been lowered to 5 kHz. Notice that f
s, 2f
s, 3f
s ... along the horizontal axis are spaced closer in
(f) than in
(d). The frequency spectrum,
(f), shows the problem: the duplicated portions of the spectrum have invaded the band between zero and one-half of the sampling frequency. Although
(f) shows these overlapping frequencies as retaining their separate identity, in actual practice they add together forming a single confused mess. Since there is no way to separate the overlapping frequencies, information is lost, and the original signal cannot be reconstructed. This overlap occurs when the analog signal contains frequencies greater than one-half the sampling rate, that is, we have proven the sampling theorem.