A lot can be said about how to measure loudspeaker Thiele/Small parameters. There are different methods of measurement and they are not all equally good (this will not be discussed here). Due to drive unit non-linearities, there is not one final set of parameters for any drive unit. Several of the parameters are a function of cone/voice coil excursion, hence they depend on the input voltage/current level. At SB Acoustics we use the delta mass method (as opposed to delta compliance). We use a constant voltage source and a 150 Ω resistor in series with the drive unit. Hence, this is neither a constant voltage nor a constant current measurement (the value of the resistor is not nearly large enough to approximate constant current, which is not the intention either).
Prior to measuring T/S parameters, the drive unit should be broken in – for two reasons. If the suspension of the drive unit is not broken in, its compliance will slightly increase during the measurement, thus affecting/distorting the results. Furthermore, eventually the drive unit will end up being broken in (it actually does not take that long), which is why it is recommended to use T/S parameters that apply for a broken-in drive unit when calculating box volumes and tuning frequencies. The free air resonance frequency typically drops about 10-15% during break-in, as the suspension compliance increases. This directly affects the Q-factors and the equivalent volume.
To break in a drive unit, you are going to need a sine wave or a noise generator with adjustable output voltage (the former is recommendable) and a power amplifier. Using a sine wave generator, adjust the frequency somewhere below the expected free air resonance frequency of the drive unit (typically about 80% of this value). Slowly turn up the voltage until the suspension reaches maximum displacement. Keep it below clipping level. Usually you can hear when the suspension goes into clipping mode - there will be some kind of mechanical noise. Adjust the voltage slightly below this level. During the process of breaking in the drive unit, it might be necessary to turn down the voltage a little to keep it from clipping, as the suspension softens. It needs to run for about ten minutes. Before measuring, let the drive unit cool to ambient temperature.
You are now ready to measure the T/S parameters. First measure the voice coil DC resistance, Re. It is recommended to use a 4-wire ohm-meter (which is quite expensive), in which case the lead wire resistance is eliminated. You can also use a really good multimeter, but be advised that many low- and mid-priced multimeters will not do the job very well. It needs to have a low resistance range (like 0-20 Ω). It is advisable not to use the lead wires that come with the multimeter when using the lower range, as the quality of these wires is often too poor. Accuracy should be better than ±0.1 Ω, which requires offset correction. Resistance is dependent on temperature. A copper voice coil that measures 6.2 Ω at 25 °C will only measure 6.07 Ω at 20 °C. SB Acoustics specifies voice coil DCresistance at 25 °C and our tolerance is ±0.15 Ω or ±2% (larger value applies).
In order to avoid unwanted mechanical resonances that may affect the results, the drive unit should be held firmly in free air in a vertical position. Make sure not to seal any vent in the pole piece. Therefore, do not place the drive unit on the floor (which would also make it resonate at some frequency). Furthermore, the drive unit should not be placed near a reflective surface, such as a wall, as this will change the radiation impedance – and we want this to be a free air measurement.
The next step is to measure the impedance curve (i.e. modulus of the impedance). To do this, you need some kind of measurement system. At SB Acoustics we use a stepped sine sweep with narrow frequency spacing (at least 1/24 oct. is recommended). High frequency resolution is crucial in order to be able to accurately determine the free air resonance frequency and the maximum impedance at this frequency – especially with high-Qms drive units. If it looks like the top of the impedance peak has been chopped off, you need more measurement points. The voltage that should be applied to the terminals of the drive unit depends on its size/type. For a typical mid-woofer, the voltage should be about 1 V (rms) at the resonance frequency.
Picture 1: The impedance-frequency curve
Notice, only SI-units are used in the following equations. Results may be converted into other units afterwards. Determine the free air resonance frequency, fs [Hz]. Determine the maximum impedance level (at the free air resonance frequency), Zmax [Ω].
Calculate the impedance level, Z1,2 [Ω], at the side frequencies.
Z1,2 = sqrt(Re * Zmax)
Determine the side frequencies (these are not the quadrant frequencies!), f1 and f2 [Hz]. Verify:
fs = sqrt(f1*f2)
Deviation from the measured value indicates drive unit non-linearities (or an inaccurate measurement). Calculate the mechanical Q-factor, Qms.
Qms = (fs/(f2 - f1))*sqrt(R0)
Where:
R0 = Zmax/Re
Calculate the electrical Q-factor, Qes:
Qes = Qms/(R0 - 1)
Calculate the total Q-factor, Qts:
Qts = Qms*Qes/(Qms + Qes)
Now attach an accurately weighed amount of sticky material (e.g. plasticine), ∆m [kg], to the center part of the cone or to the dust cap (be careful not to damage the dust cap). Do not be tempted to use small magnets on either side of the cone as added mass, as this will affect the measurement results. Add about 70% of the expected moving mass of the drive unit. Make sure that the entire added mass sticks to the cone, so that no part of it can vibrate freely. Notice that removal of sticky material may cause certain types of paper cones to delaminate in the top layers.
Once again measure the impedance curve - do not adjust the voltage (or current). Determine the new/shifted resonance frequency, fo [Hz]. Calculate the moving mass (incl. air), mms [kg].
mms = ∆m/((fs/f0)^2 - 1)
Calculate the mechanical (loss) resistance, Rms [kg/s]:
Rms = 2πfs*mms/Qms
Calculate the force factor, BL [Tm]:
BL = sqrt((Zmax - Re)*Rms)
Calculate the compliance of the suspension, Cms [m/N]:
Cms = 1/(2πfs)^2 * mms
Measure the piston diameter (as shown on the Picture 2 below), Dd [m].
Picture 2: Piston diameter
Calculate the piston area, Sd [m2]:
Sd = π * (Dd/2)^2
The effective piston area is approximately 95% of the above calculated value in most cases. Hence, a correction should be made. A correction must also be made if the drive unit uses a porous/vented dust cap or a phase plug, obviously. Calculate the equivalent volume, Vas [m3]:
Vas = Cms * ρ * c^2 * Sd^2
Where:
ρ is the density of air, ρ = 1.2 kg/m3 (20 °C, 50% RH, 1 atm);
c is the speed of sound in air, c = 344 m/s (20 °C, 50% RH).
Determine the minimum impedance level above the resonance frequency, Zmin [Ω]. Determine the frequency, f3 [Hz], at which the impedance level is 3 dB above Zmin (3 dB is a factor of √2).
Calculate the voice coil inductance, Le [H]. An empirical equation is used, as a voice coil sitting in a motor system does not behave like a true inductor. This model for voice coil inductance is rather simple – better lumped models have been made.
Le = ((Re*20*10^3)/2πf3 + 0.5)*10^-3/20
The set of Thiele/Small parameters now is complete.
Source: SB Acoustics.
Thiele-Small Parameters
In the early seventies, several technical papers were presented to the AES (Audio Engineering Society) that resulted in the development of what we know today as ‘Thiele-Small Parameters’. These papers were authored by A.N.Thiele and Richard H. Small. Thiele was the senior engineer of design and development for the Australian Broadcasting Commission and was responsible at the time for the Federal Engineering Laboratory, as well as for analyzing the design of equipment and systems for sound and vision broadcasting. Small was, at the time, a Commonwealth Post-graduate Research Student in the School of Electrical Engineering at the University of Sydney.
This parameter is the free-air resonant frequency of a speaker. It is the frequency where the driver moves with minimal effort. In other words, it is the point at which the weight of the moving parts of the speaker becomes balanced with the force of the speaker suspension when in motion. If you’ve ever seen a piece of string start humming uncontrollably in the wind, you have seen the effect of reaching a resonant frequency. It is important to know this information so that you can prevent your enclosure from ‘ringing’. If you tap a speaker (or any object for that matter), it will make a sound, which has the same frequency as its resonant frequency. With a loudspeaker, the mass of the moving parts, and the stiffness of the suspension (surround and spider) are the key elements that affect the resonant frequency. When the driver reaches the resonance frequency, its response starts to roll off. As a general rule of thumb, a lower Fs indicates a woofer that would be better for low-frequency reproduction than a woofer with a higher Fs. This is not always the case though, because other parameters affect the ultimate performance as well. The lower the Fs , the better. A woofer with Fs of 50 Hz will not play well at 40 Hz, and a woofer with Fs of 30 Hz will play well at 40 Hz. Woofers can have resonant frequencies of 20 Hz or even lower. While you can’t hear those frequencies, you can feel them. Fs for midrange drivers and tweeters is irrelevant, as they will probably play above that frequency anyway.
The Re parameter is the DC resistance of the driver measured with an ohm meter and it is often referred to as the ‘DCR’. This measurement will almost always be less than the driver’s nominal impedance. Consumers sometimes get concerned the Re is less than the published impedance and fear that amplifiers will be overloaded. Due to the fact that the inductance of a speaker rises with a rise in frequency, it is unlikely that the amplifier will often see the DC resistance as its load.
This is the voice coil inductance measured in millihenries (mH). The industry standard is to measure inductance at 1 kHz. As frequencies get higher there will be a rise in impedance above Re. This is because the voice coil is acting as an inductor. Consequently, the impedance of a speaker is not a fixed resistance, but can be represented as a curve that changes as the input frequency changes. Maximum impedance (Zmax) occurs at Fs. When current is applied to the voice coil, at the same time, an additional current flow is created, in the opposite direction of the current flow, called back EMF, which is short for electromotive force. As current flows through the voice coil, it moves it into a certain direction, and back EMF tries to move it in the opposite direction. That is why the impedance spikes at resonance frequency. At that frequency the speaker easily reaches high excursions and back EMF is working hard to pull it back. Inductance causes the impedance to rise as the frequency goes up. Large Le values will translate into poor high frequency response. To improve the high frequency response, a technique called shorting ring or Faraday loop can be used, but that's another subject for discussion.
The impedance is the AC resistance, which is not a fixed value because the speaker is moving and the impedance varies with frequency. Impedance will have a high value at resonance frequency. Usually the manufacturers quote one number, like 4, 6 or 8 ohms. A 8 ohm speaker can have impedance vary from 6 ohms to 25 ohms or more, but for the most frequencies it will be around 8 ohms.
The Bl parameter is product of B, which is the flux density, and l, which is the length of the voice coil. In other words, this is a measurement of the motor strength of a speaker. Think of this as how good a weightlifter the transducer is. A measured mass is applied to the cone forcing it back while the current required for the motor to force the mass back is measured. The formula is mass in grams divided by the current in amperes. A higher Bl will translate in higher efficiency. Of course, the efficiency is determined by lots of factors, so a higher Bl doesn’t necessarily mean a higher SPL. To get the bigger picture, the bigger magnet and bigger coil equals bigger motor. Neodymium magnets are stronger than normal ferrite magnets and they don’t need to be as large. The strength of the motor is in direct correlation with the size and the weight of the cone, size of the coil, size of the magnet, size of the basket. If we modify Bl, that will change a lot of things. A high Bl speaker will be suitable for loaded horn applications. Also, a high Bl will translate into better transients (sudden sounds). The motor has enough power to move the cone with a fast reaction time. Bl is in accordance with the size of the speaker, so it’s hard to give an estimate of which is high and which is low. Bl of around 10 is pretty average.
Qms, Qes and Qts are measurements related to the control of a transducer’s suspension when it reaches the resonant frequency (Fs). The suspension must prevent any lateral motion that might allow the voice coil and pole to touch (this would destroy the loudspeaker). The suspension must also act like a shock absorber.
Qts of values of 0.6 or higher, will demand a very large box. The predefined bass-reflex alignments can be used for Qts values lower than 0.7. Higher Qes values suggests that the woofer is more suitable for sealed enclosures, while lower values recommends the bass-reflex. As a general guideline, Qts of 0.4 or below indicates a transducer well suited to a vented enclosure. Qts between 0.4 and 0.7 indicates suitability for a sealed enclosure. Qts of 0.7 or above indicates suitability for free-air or infinite baffle applications. However, there are exceptions.
Cms is the compliance of the speaker. Cms is measured in meters per Newton. Cms is the force exerted by the mechanical suspension of the speaker. It is simply a measurement of its stiffness. The suspension of the speaker (the surround and the spider) has a certain stiffness. If the suspension is stiff, the driver is not compliant. So, the easy it is to move the speaker, the more compliant it is. Considering stiffness (Cms), in conjunction with the Q parameters gives rise to the kind of subjective decisions made by car manufacturers when tuning cars between comfort to carry the president and precision to go racing. Think of the peaks and valleys of audio signals like a road surface then consider that the ideal speaker suspension is like car suspension that can traverse the rockiest terrain with race-car precision and sensitivity at the speed of a fighter plane. It’s quite a challenge because focusing on any one discipline tends to have a detrimental effect on the others.
Compliance affects the resonant frequency. A higher Cms will yield a lower Fs. If Cms goes up => Fs goes down. Like, for example, a ball on a spring. The stiffness of the spring determines the compliance. If the spring is stiff, then it is less compliant and the ball will bounce at a higher frequency (short and fast bounces). If the spring is not stiff, or more compliant, the ball will make long bounces - reduced frequency.
Vas represents the volume of air that when compressed to one cubic meter exerts the same force as the compliance (Cms) of the suspension in a particular speaker. The air inside the cabinet has its own compliance. When you try to compress the air inside a box, you will encounter resistance. If the box is small, the air is harder to compress and therefore less compliant, and if the box is larger, the air is easier to compress, therefore more compliant. In conclusion, Vas describes the volume of the air inside the cabinet, where the compliance of the speaker matches the compliance of the air inside the box. Vas is one of the trickiest parameters to measure because air pressure changes relative to humidity and temperature — a precisely controlled lab environment is essential.
Short for Maximum Linear Excursion. Speaker output becomes non-linear when the voice coil begins to leave the magnetic gap. Although suspensions can create non-linearity in output, the point at which the number of turns in the gap (see BL) begins to decrease is when distortion starts to increase. Xmax is the maximum distance a speaker can travel without distorting. The coil has a certain length and moves up and down inside the magnetic gap of the motor. If the coil travels too far and leaves the magnetic gap, the speaker will distort, as the magnet has a reduced control on the voice coil. Don’t confuse this Thiele/Small parameter with Xmech.
Xmax = ((height of the voice coil) – (height of the magnetic gap)) / 2
Is the maximum distance a speaker can travel without damaging the driver. When a driver is exceeding the quoted Xmax, distortion is introduced into the sound. However, if the driver exceeds the quoted Xmech, the mechanical limits of the driver are reached and damage can occur to the driver. When the driver travels forward, it will stretch the surround until it can’t move forward. It looks and sounds disturbing. On the way back, the voice coil will hit the back plate of the magnet and will sound like loud bangs/knocks. The exceeded Xmech of the speaker can damage it.
The effective area of the cone or the actual surface area of the cone, normally given in square cm. This is important, if you want to reach high pressure levels (Xmax also). You are probably wandering why 2 speakers of the same quoted dimensions have different Sd ? It is because only half of the surround is considered cone area, so larger surrounds will yield a smaller Sd.
This parameter is the Peak Diaphragm Displacement Volume — in other words the volume of air the cone will move. It is calculated by multipying Xmax (Voice Coil Overhang of the driver) by Sd (Surface area of the cone).
This parameter is the combination of the weight of the cone assembly plus the ‘driver radiation mass load’. The weight of the cone assembly is easy: it’s just the sum of the weight of the cone assembly components. The driver radiation mass load is the confusing part. In simple terminology, it is the weight of the air (the amount calculated in Vd) that the cone will have to push.
This measurement is calculated by dividing Fs by Qes. The EBP figure is used in many enclosure design formulas to determine if a speaker is more suitable for a closed or vented design. An EBP close to 100 usually indicates a speaker that is best suited for a vented enclosure. On the contrary, an EBP closer to 50 usually indicates a speaker best suited for a closed box design. This is merely a starting point. Many well-designed systems have violated this rule of thumb! Qts should also be considered.
This is the total moving mass. If you place on a scale the cone, the coil, half of the surround and half of the spider, you got yourself the value of Mmd. If you add to this equation the weight of the air in front of the speaker, then you will get the Mms value. When the speaker is moving, the pocket of air directly in front of it, will move with the cone. This air has its own mass and has to be accounted for, when calculating the total moving mass (Mms). If Mms goes up, the Fs goes down (imagine a ball hanging on a spring. If the ball is heavier, the ball will bounce at a lower frequency). If Mms goes up, the efficiency goes down (more amplifier power is needed to push the cone).
SPL stands for sound pressure level. The higher the number, the higher the efficiency. Good SPL rating is around 88 – 90 db, at 1 W / 1 m. This means that the manufacturer picks a certain frequency (depending on the type of the driver : woofer, midrange, tweeter), places a microphone at 1 meter from the speaker, and plays a 1 W tone at that frequency. How many decibels the microphone picks up is the actual SPL. The higher the efficiency, the better. This takes impedance into account. At 8 ohms there is no difference. So 90 db measured at 2.83 V / 1 m are the same as 90 db measured at 1 W / 1 m. But if the speaker is 4 ohms, 90 db measured at 2.83 V / 1 m is equal to 90 db measured at 2 W / 1 m, which is equivalent to 87 db 1 W / 1m. For a 2 ohm speaker 90 db 2.83 V / 1 m is equivalent to 84 db 1 W / 1 m and so on.
This is the frequency range for which Eminence feels the transducer will prove useful. Manufacturers use different techniques for determining ‘Usable Frequency Range’. Most methods are recognized as acceptable in the industry, but can arrive at different results. Technically, many loudspeakers are used to produce frequencies in ranges where they would theoretically be of little use. As frequencies increase, the off-axis coverage of a transducer decreases relative to its diameter. At a certain point, the coverage becomes ‘beamy’ or narrow like the beam of a flashlight. If you’ve ever stood in front of a guitar amplifier or speaker cabinet, then moved slightly to one side or the other and noticed a different sound, you have experienced this phenomenon and are now aware of why it occurs. Clearly, most two-way enclosures ignore the theory and still perform quite well. The same is true for many guitar amplifiers, but it is useful to know at what point you can expect a compromise in coverage.
This specification is very important to transducer selection. Obviously, you need to choose a loudspeaker that is capable of handling the input power you are going to provide. By the same token, you can destroy a loudspeaker by using too little power. The ideal situation is to choose a loudspeaker that has the capability of handling more power than you can provide lending some headroom and insurance against thermal failure. To use an automobile as an analogy; you would not buy a car that could only go 55mph if that were the speed you always intended to drive. Generally speaking, the number one contributor to a transducer’s power rating is its ability to release thermal energy. This is affected by several design choices, but most notably voice coil size, magnet size, venting, and the adhesives used in voice coil construction. Larger coil and magnet sizes provide more area for heat to dissipate, while venting allows thermal energy to escape and cooler air to enter the motor structure. Equally important is the ability of the voice coil to handle thermal energy. Eminence is renowned for its use of proprietary adhesives and components that maximize the voice coil’s ability to handle extreme temperatures. Mechanical factors must also be considered when determining power handling. A transducer might be able to handle 1,000W from a thermal perspective, but would fail long before that level was reached from a mechanical issue such as the coil hitting the back plate, the coil coming out of the gap, the cone buckling from too much outward movement, or the spider bottoming on the top plate. The most common cause of such a failure would be asking the speaker to produce more low frequencies than it could mechanically produce at the rated power. Be sure to consider the suggested usable frequency range and the Xlim parameter in conjunction with the power rating to avoid such failures. The Eminence power rating is derived using an EIA 426A noise source and test standard. All tests are conducted for eight hours in a free-air, non-temperature controlled environment. Eminence tests samples from each of three different production runs and each sample must pass a test exceeding the rated power by 50 to 100W. The Eminence music program is double that of our standard Watts rating.
This data represents one of the most useful specifications published for any transducer. It is a representation of the efficiency and volume you can expect from a device relative to the input power. Loudspeaker manufacturers follow different rules when obtaining this information — there is not an exact standard accepted by the industry. As a result, it is often the case that loudspeaker buyers are unable to compare ‘apples to apples’ when looking at the sensitivities of different manufacturers’ products. Eminence sensitivities are expressed as the average output across the usable frequency when applying 1W/1M into the nominal impedance. ie: 2.83V/8 ohms, 4V/16 ohms.
Fs = 50*Pi*sqrt(1/(Cms*Mms))
Units of measurement:
Fs in Hz;
Cms in mm/N (millimeters/newton);
Mms in g (grams).
Altering the compliance or the moving mass will directly affect the resonant frequency:
>> Increasing Cms will decrease Fs. This can be done by making the suspension looser.
>> Increasing Mms will decrease Fs. This can be done by choosing a heavier material for the cone.
Vas = 0.0014 * Sd^2 * Cms
Units of measurement:
Vas in l (liters);
Sd in cm^2;
Cms in mm/N.
Increasing the size of the speaker or the compliance (looser suspension) will increase Vas as a result.
Res = Z0 – Re
Qms = Res / (BL^2 * Cms * 6.283 * Fs)
Qes = Re / (BL^2 * Cms * 6.283 * Fs)
Units of measurement:
Res is calculated by subtracting the voice coil resistance (Re) from the impedance peak measured at resonance (Z0) – all measured in ohms;
BL in Tm (Tesla * meters);
Cms in m/N (meters/newton);
Fs in Hz.
Qts = (Qes * Qms) / (Qes + Qms)
Calculate Qts by adding Qes and Qms like resistances in parallel.
Conclusions: Increasing BL, Cms or Fs will reduce Qes and Qms. Increasing Re will result in increasing Qes. This can be done by adding a series resistor, but this will also affect the efficiency of the driver in a negative way. A higher impedance peak at resonance will translate in a higher Qms.
Mmr – the air mass load – the air in front of the cone that follows the cone motion;
Mmd – the assembly mass – the mass of all the components that move (cone, voice coil, half of the surround, half of the spider).
Here are the equations for calculating the moving mass:
Mmr = 0.000575 * Sd^1.5
Mms = Mmd + Mmr
Units of measurement: the masses are in grams and Sd is in cm^2.
Clearly the air mass load is highly dependent on the size of the speaker. The moving mass is the sum of the assembly mass and the air mass load.
Le = 1.592 * 10^-5 * (R10k – Re^2)^1/2
Where R10k is the resistance at 10 kHz measured in ohms, and Re is the DC resistance measured in ohms.
n0 = (9.7822 * 10^-10 * Vas * Fs^3) / Qes
n0 above is a ratio, not a percentage. To make it a percentage multiply by 100;
Vas is in liters;
Fs in Hz;
SPL @ 1W/1m = 112.2 + 10 * log(n0)
The SPL rating is in direct proportion to n0. Important to note is that the efficiency coefficient (n0) is highly dependent to the resonant frequency, because it’s at the power of 3. In conclusion, tweeters and mid-range drivers will be more efficient versus subwoofers.
Fs (Hz)
This parameter is the free-air resonant frequency of a speaker. It is the frequency where the driver moves with minimal effort. In other words, it is the point at which the weight of the moving parts of the speaker becomes balanced with the force of the speaker suspension when in motion. If you’ve ever seen a piece of string start humming uncontrollably in the wind, you have seen the effect of reaching a resonant frequency. It is important to know this information so that you can prevent your enclosure from ‘ringing’. If you tap a speaker (or any object for that matter), it will make a sound, which has the same frequency as its resonant frequency. With a loudspeaker, the mass of the moving parts, and the stiffness of the suspension (surround and spider) are the key elements that affect the resonant frequency. When the driver reaches the resonance frequency, its response starts to roll off. As a general rule of thumb, a lower Fs indicates a woofer that would be better for low-frequency reproduction than a woofer with a higher Fs. This is not always the case though, because other parameters affect the ultimate performance as well. The lower the Fs , the better. A woofer with Fs of 50 Hz will not play well at 40 Hz, and a woofer with Fs of 30 Hz will play well at 40 Hz. Woofers can have resonant frequencies of 20 Hz or even lower. While you can’t hear those frequencies, you can feel them. Fs for midrange drivers and tweeters is irrelevant, as they will probably play above that frequency anyway.
Re (Ohms)
The Re parameter is the DC resistance of the driver measured with an ohm meter and it is often referred to as the ‘DCR’. This measurement will almost always be less than the driver’s nominal impedance. Consumers sometimes get concerned the Re is less than the published impedance and fear that amplifiers will be overloaded. Due to the fact that the inductance of a speaker rises with a rise in frequency, it is unlikely that the amplifier will often see the DC resistance as its load.
Le (mH)
This is the voice coil inductance measured in millihenries (mH). The industry standard is to measure inductance at 1 kHz. As frequencies get higher there will be a rise in impedance above Re. This is because the voice coil is acting as an inductor. Consequently, the impedance of a speaker is not a fixed resistance, but can be represented as a curve that changes as the input frequency changes. Maximum impedance (Zmax) occurs at Fs. When current is applied to the voice coil, at the same time, an additional current flow is created, in the opposite direction of the current flow, called back EMF, which is short for electromotive force. As current flows through the voice coil, it moves it into a certain direction, and back EMF tries to move it in the opposite direction. That is why the impedance spikes at resonance frequency. At that frequency the speaker easily reaches high excursions and back EMF is working hard to pull it back. Inductance causes the impedance to rise as the frequency goes up. Large Le values will translate into poor high frequency response. To improve the high frequency response, a technique called shorting ring or Faraday loop can be used, but that's another subject for discussion.
Impedance (Ohms)
The impedance is the AC resistance, which is not a fixed value because the speaker is moving and the impedance varies with frequency. Impedance will have a high value at resonance frequency. Usually the manufacturers quote one number, like 4, 6 or 8 ohms. A 8 ohm speaker can have impedance vary from 6 ohms to 25 ohms or more, but for the most frequencies it will be around 8 ohms.
Bl (Tm)
The Bl parameter is product of B, which is the flux density, and l, which is the length of the voice coil. In other words, this is a measurement of the motor strength of a speaker. Think of this as how good a weightlifter the transducer is. A measured mass is applied to the cone forcing it back while the current required for the motor to force the mass back is measured. The formula is mass in grams divided by the current in amperes. A higher Bl will translate in higher efficiency. Of course, the efficiency is determined by lots of factors, so a higher Bl doesn’t necessarily mean a higher SPL. To get the bigger picture, the bigger magnet and bigger coil equals bigger motor. Neodymium magnets are stronger than normal ferrite magnets and they don’t need to be as large. The strength of the motor is in direct correlation with the size and the weight of the cone, size of the coil, size of the magnet, size of the basket. If we modify Bl, that will change a lot of things. A high Bl speaker will be suitable for loaded horn applications. Also, a high Bl will translate into better transients (sudden sounds). The motor has enough power to move the cone with a fast reaction time. Bl is in accordance with the size of the speaker, so it’s hard to give an estimate of which is high and which is low. Bl of around 10 is pretty average.
Q Parameters
Qms, Qes and Qts are measurements related to the control of a transducer’s suspension when it reaches the resonant frequency (Fs). The suspension must prevent any lateral motion that might allow the voice coil and pole to touch (this would destroy the loudspeaker). The suspension must also act like a shock absorber.
Q (Unitless)
Also called quality factor or damping factor. The damping of the speaker, is a characteristic that helps the speaker to resume its rest state. Without adequate damping, a speaker would move uncontrollably at resonance frequency. Q actually stands for quality factor and is the inverse of damping. As damping goes up, Q goes down, but it is widely accepted that Q is a measurement of damping. There are 3 types of speaker damping: mechanical, electrical and pneumatic.Qms
Qms is the mechanical Q or the damping made by the suspension of the driver: the surround and the spider of the speaker. Qms is a measurement of the control coming from the speaker’s mechanical suspension system (the surround and spider). View these components like springs.Qes
Qes is the electrical Q or the damping made by the coil – magnet assembly. Qes is a measurement of the control coming from the speaker’s electrical suspension system (the voice coil and magnet). Opposing forces from the mechanical and electrical suspensions act to absorb the shock. When the coil moves through the magnetic field, it generates a current which opposes this motion (hence the electrical damping). Another factor which contributes to the electrical damping is the amplifier. This depends on the particular amplifier. The Qes provided by the speaker manufacturer does not include amplifier damping.Qts
Also called total Q – The damping made by Qms and Qes combined. Qts is called the ‘Total Q’ of the driver and is derived from an equation where Qes is multiplied by Qms and the result is divided by the sum of the same: 1/Qts = 1/Qms + 1/Qes. This is the Q we should look for if we plan to use it in the free air.Qtc
This is the pneumatic damping. This parameter exists only when there is a box in the equation. Depending on the size of the box, the air inside it will act like a spring and contribute to the dampening of the speaker. You can say that Qtc = Qts + Q of the box. This is the Q we should look for if we plan to use a sealed box.Qts of values of 0.6 or higher, will demand a very large box. The predefined bass-reflex alignments can be used for Qts values lower than 0.7. Higher Qes values suggests that the woofer is more suitable for sealed enclosures, while lower values recommends the bass-reflex. As a general guideline, Qts of 0.4 or below indicates a transducer well suited to a vented enclosure. Qts between 0.4 and 0.7 indicates suitability for a sealed enclosure. Qts of 0.7 or above indicates suitability for free-air or infinite baffle applications. However, there are exceptions.
Cms (m/N)
Cms is the compliance of the speaker. Cms is measured in meters per Newton. Cms is the force exerted by the mechanical suspension of the speaker. It is simply a measurement of its stiffness. The suspension of the speaker (the surround and the spider) has a certain stiffness. If the suspension is stiff, the driver is not compliant. So, the easy it is to move the speaker, the more compliant it is. Considering stiffness (Cms), in conjunction with the Q parameters gives rise to the kind of subjective decisions made by car manufacturers when tuning cars between comfort to carry the president and precision to go racing. Think of the peaks and valleys of audio signals like a road surface then consider that the ideal speaker suspension is like car suspension that can traverse the rockiest terrain with race-car precision and sensitivity at the speed of a fighter plane. It’s quite a challenge because focusing on any one discipline tends to have a detrimental effect on the others.
Compliance affects the resonant frequency. A higher Cms will yield a lower Fs. If Cms goes up => Fs goes down. Like, for example, a ball on a spring. The stiffness of the spring determines the compliance. If the spring is stiff, then it is less compliant and the ball will bounce at a higher frequency (short and fast bounces). If the spring is not stiff, or more compliant, the ball will make long bounces - reduced frequency.
Vas (l)
Vas represents the volume of air that when compressed to one cubic meter exerts the same force as the compliance (Cms) of the suspension in a particular speaker. The air inside the cabinet has its own compliance. When you try to compress the air inside a box, you will encounter resistance. If the box is small, the air is harder to compress and therefore less compliant, and if the box is larger, the air is easier to compress, therefore more compliant. In conclusion, Vas describes the volume of the air inside the cabinet, where the compliance of the speaker matches the compliance of the air inside the box. Vas is one of the trickiest parameters to measure because air pressure changes relative to humidity and temperature — a precisely controlled lab environment is essential.
Xmax (mm)
Short for Maximum Linear Excursion. Speaker output becomes non-linear when the voice coil begins to leave the magnetic gap. Although suspensions can create non-linearity in output, the point at which the number of turns in the gap (see BL) begins to decrease is when distortion starts to increase. Xmax is the maximum distance a speaker can travel without distorting. The coil has a certain length and moves up and down inside the magnetic gap of the motor. If the coil travels too far and leaves the magnetic gap, the speaker will distort, as the magnet has a reduced control on the voice coil. Don’t confuse this Thiele/Small parameter with Xmech.
Xmax = ((height of the voice coil) – (height of the magnetic gap)) / 2
Xmech (mm)
Is the maximum distance a speaker can travel without damaging the driver. When a driver is exceeding the quoted Xmax, distortion is introduced into the sound. However, if the driver exceeds the quoted Xmech, the mechanical limits of the driver are reached and damage can occur to the driver. When the driver travels forward, it will stretch the surround until it can’t move forward. It looks and sounds disturbing. On the way back, the voice coil will hit the back plate of the magnet and will sound like loud bangs/knocks. The exceeded Xmech of the speaker can damage it.
Sd (m^2)
The effective area of the cone or the actual surface area of the cone, normally given in square cm. This is important, if you want to reach high pressure levels (Xmax also). You are probably wandering why 2 speakers of the same quoted dimensions have different Sd ? It is because only half of the surround is considered cone area, so larger surrounds will yield a smaller Sd.
Vd
This parameter is the Peak Diaphragm Displacement Volume — in other words the volume of air the cone will move. It is calculated by multipying Xmax (Voice Coil Overhang of the driver) by Sd (Surface area of the cone).
MMS
This parameter is the combination of the weight of the cone assembly plus the ‘driver radiation mass load’. The weight of the cone assembly is easy: it’s just the sum of the weight of the cone assembly components. The driver radiation mass load is the confusing part. In simple terminology, it is the weight of the air (the amount calculated in Vd) that the cone will have to push.
EBP
This measurement is calculated by dividing Fs by Qes. The EBP figure is used in many enclosure design formulas to determine if a speaker is more suitable for a closed or vented design. An EBP close to 100 usually indicates a speaker that is best suited for a vented enclosure. On the contrary, an EBP closer to 50 usually indicates a speaker best suited for a closed box design. This is merely a starting point. Many well-designed systems have violated this rule of thumb! Qts should also be considered.
Mms and Mmd (g)
This is the total moving mass. If you place on a scale the cone, the coil, half of the surround and half of the spider, you got yourself the value of Mmd. If you add to this equation the weight of the air in front of the speaker, then you will get the Mms value. When the speaker is moving, the pocket of air directly in front of it, will move with the cone. This air has its own mass and has to be accounted for, when calculating the total moving mass (Mms). If Mms goes up, the Fs goes down (imagine a ball hanging on a spring. If the ball is heavier, the ball will bounce at a lower frequency). If Mms goes up, the efficiency goes down (more amplifier power is needed to push the cone).
SPL (dB)
SPL stands for sound pressure level. The higher the number, the higher the efficiency. Good SPL rating is around 88 – 90 db, at 1 W / 1 m. This means that the manufacturer picks a certain frequency (depending on the type of the driver : woofer, midrange, tweeter), places a microphone at 1 meter from the speaker, and plays a 1 W tone at that frequency. How many decibels the microphone picks up is the actual SPL. The higher the efficiency, the better. This takes impedance into account. At 8 ohms there is no difference. So 90 db measured at 2.83 V / 1 m are the same as 90 db measured at 1 W / 1 m. But if the speaker is 4 ohms, 90 db measured at 2.83 V / 1 m is equal to 90 db measured at 2 W / 1 m, which is equivalent to 87 db 1 W / 1m. For a 2 ohm speaker 90 db 2.83 V / 1 m is equivalent to 84 db 1 W / 1 m and so on.
Usable frequency range
This is the frequency range for which Eminence feels the transducer will prove useful. Manufacturers use different techniques for determining ‘Usable Frequency Range’. Most methods are recognized as acceptable in the industry, but can arrive at different results. Technically, many loudspeakers are used to produce frequencies in ranges where they would theoretically be of little use. As frequencies increase, the off-axis coverage of a transducer decreases relative to its diameter. At a certain point, the coverage becomes ‘beamy’ or narrow like the beam of a flashlight. If you’ve ever stood in front of a guitar amplifier or speaker cabinet, then moved slightly to one side or the other and noticed a different sound, you have experienced this phenomenon and are now aware of why it occurs. Clearly, most two-way enclosures ignore the theory and still perform quite well. The same is true for many guitar amplifiers, but it is useful to know at what point you can expect a compromise in coverage.
Power handling
This specification is very important to transducer selection. Obviously, you need to choose a loudspeaker that is capable of handling the input power you are going to provide. By the same token, you can destroy a loudspeaker by using too little power. The ideal situation is to choose a loudspeaker that has the capability of handling more power than you can provide lending some headroom and insurance against thermal failure. To use an automobile as an analogy; you would not buy a car that could only go 55mph if that were the speed you always intended to drive. Generally speaking, the number one contributor to a transducer’s power rating is its ability to release thermal energy. This is affected by several design choices, but most notably voice coil size, magnet size, venting, and the adhesives used in voice coil construction. Larger coil and magnet sizes provide more area for heat to dissipate, while venting allows thermal energy to escape and cooler air to enter the motor structure. Equally important is the ability of the voice coil to handle thermal energy. Eminence is renowned for its use of proprietary adhesives and components that maximize the voice coil’s ability to handle extreme temperatures. Mechanical factors must also be considered when determining power handling. A transducer might be able to handle 1,000W from a thermal perspective, but would fail long before that level was reached from a mechanical issue such as the coil hitting the back plate, the coil coming out of the gap, the cone buckling from too much outward movement, or the spider bottoming on the top plate. The most common cause of such a failure would be asking the speaker to produce more low frequencies than it could mechanically produce at the rated power. Be sure to consider the suggested usable frequency range and the Xlim parameter in conjunction with the power rating to avoid such failures. The Eminence power rating is derived using an EIA 426A noise source and test standard. All tests are conducted for eight hours in a free-air, non-temperature controlled environment. Eminence tests samples from each of three different production runs and each sample must pass a test exceeding the rated power by 50 to 100W. The Eminence music program is double that of our standard Watts rating.
Sensitivity
This data represents one of the most useful specifications published for any transducer. It is a representation of the efficiency and volume you can expect from a device relative to the input power. Loudspeaker manufacturers follow different rules when obtaining this information — there is not an exact standard accepted by the industry. As a result, it is often the case that loudspeaker buyers are unable to compare ‘apples to apples’ when looking at the sensitivities of different manufacturers’ products. Eminence sensitivities are expressed as the average output across the usable frequency when applying 1W/1M into the nominal impedance. ie: 2.83V/8 ohms, 4V/16 ohms.
Formulas:
Fs – Resonant frequency
According to the ball hooked up to a spring analogy, the ball will bounce differently (frequency) depending on how heavy the ball is or how stiff the spring is. If the ball is heavy, it will take long bounces. Therefore, reduced frequency, as it takes longer to complete a cycle. However, if the spring is stiffer, it pulls the ball back faster. In conclusion, higher frequency. Since we’re talking about Thiele/Small parameters equations, here is the equation for the resonant frequency:Fs = 50*Pi*sqrt(1/(Cms*Mms))
Units of measurement:
Fs in Hz;
Cms in mm/N (millimeters/newton);
Mms in g (grams).
Altering the compliance or the moving mass will directly affect the resonant frequency:
>> Increasing Cms will decrease Fs. This can be done by making the suspension looser.
>> Increasing Mms will decrease Fs. This can be done by choosing a heavier material for the cone.
Vas – Equivalent compliance in liters
Vas expresses the compliance of the speaker in terms of volume. Imagine a syringe without the needle. Close up the nozzle with your finger. If you try to push the plunger, you will encounter resistance from the air trapped inside the tube. This amount of air has a certain compliance. If the syringe is bigger (higher volume of air), the air is easier to compress, therefore, higher compliance. Having said this analogy, Vas is the compliance of the speaker expressed in liters.Vas = 0.0014 * Sd^2 * Cms
Units of measurement:
Vas in l (liters);
Sd in cm^2;
Cms in mm/N.
Increasing the size of the speaker or the compliance (looser suspension) will increase Vas as a result.
Qes, Qms and Qts
These 3 Thiele/Small parameters equations have more to do with the interaction, rather than the calculation. To calculate them, you would use the impedance curve, rather than the following equations:Res = Z0 – Re
Qms = Res / (BL^2 * Cms * 6.283 * Fs)
Qes = Re / (BL^2 * Cms * 6.283 * Fs)
Units of measurement:
Res is calculated by subtracting the voice coil resistance (Re) from the impedance peak measured at resonance (Z0) – all measured in ohms;
BL in Tm (Tesla * meters);
Cms in m/N (meters/newton);
Fs in Hz.
Qts = (Qes * Qms) / (Qes + Qms)
Calculate Qts by adding Qes and Qms like resistances in parallel.
Conclusions: Increasing BL, Cms or Fs will reduce Qes and Qms. Increasing Re will result in increasing Qes. This can be done by adding a series resistor, but this will also affect the efficiency of the driver in a negative way. A higher impedance peak at resonance will translate in a higher Qms.
Mms – moving mass
This is one of the most obvious Thiele/Small parameters equations. First of all, let’s talk about the components of the moving mass:Mmr – the air mass load – the air in front of the cone that follows the cone motion;
Mmd – the assembly mass – the mass of all the components that move (cone, voice coil, half of the surround, half of the spider).
Here are the equations for calculating the moving mass:
Mmr = 0.000575 * Sd^1.5
Mms = Mmd + Mmr
Units of measurement: the masses are in grams and Sd is in cm^2.
Clearly the air mass load is highly dependent on the size of the speaker. The moving mass is the sum of the assembly mass and the air mass load.
Le – Inductance
Le is the voice coil inductance and it’s measured in millihenries (mH). The equation for the voice coil inductance is:Le = 1.592 * 10^-5 * (R10k – Re^2)^1/2
Where R10k is the resistance at 10 kHz measured in ohms, and Re is the DC resistance measured in ohms.
n0 and SPL rating – Efficiency
n0 is a percentage, showing how efficient the driver is at converting an electrical signal to an acoustical one. As a result, the bigger the number, the greater the reference sound pressure level.n0 = (9.7822 * 10^-10 * Vas * Fs^3) / Qes
n0 above is a ratio, not a percentage. To make it a percentage multiply by 100;
Vas is in liters;
Fs in Hz;
SPL @ 1W/1m = 112.2 + 10 * log(n0)
The SPL rating is in direct proportion to n0. Important to note is that the efficiency coefficient (n0) is highly dependent to the resonant frequency, because it’s at the power of 3. In conclusion, tweeters and mid-range drivers will be more efficient versus subwoofers.
The Michelson-Morley paradox solved
The Michelson-Morley Paradox Solved is a treatise written by Justin Jacobs. It thoroughly examines the Michelson-Morley paradoxical null results and is written in a manner that is meant to make it approachable to the general public. In this article we expose the whole Section 8 of this treatise, which is the section where the author describes the main idea of its treatise.
THE REAL AND CORRECT THEORETICAL, EMPIRICAL & TECHNICAL SOLUTIONS FOR MICHELSON’S PARADOXICAL NULL RESULTS
The first real reason for Michelson’s null results is completely theoretical. Michelson was attempting to detect the absolute velocity of the Earth through the ether by detecting a theoretical difference between two theoretical time intervals for light rays to propagate in two different directions, with respect to the ether.
There were at least nine different ether theories concerning the theoretical difference in time intervals, or why such difference was not detected:
1) Lorentz’s 1886 stationary ether theory;
2) Fresnel’s 1818 theory that the ether was being partially dragged along by the Earth;
3) George Stokes’ 1845 theory that the ether was being totally dragged along by the Earth’s motion through it;
4) Maxwell’s 1879 ether displacement theory which compared light propagation on a moving Earth and on an absolutely stationary Earth;
5) the “ether wind” theory which should decrease the velocity of light in the direction of the Earth’s solar orbital motion;
6) Michelson’s theory that the longitudinal mirror in his apparatus would displace from stationary ether and a propagating light ray in the direction of the Earth’s solar orbital motion;
7) Michelson & Morley’s theory that both mirrors in their apparatus should be displacing differently from stationary ether;
8) Fitzgerald’s and Lorentz’s theory that the time interval difference existed but it could not be detected because of a physical contraction of matter; and
9) Einstein’s theory that the difference in time intervals should result from the way time coordinates are measured.
Theoretically, several of these different ether theories should have produced a specific time interval difference for light to propagate in a certain direction. But Michelson never detected any difference in the time interval for light to propagate in any different direction of the Earth’s motion through space, nor has anyone else.
Apparently, no one has ever realized that all of these absolute theories and theoretical positions, motions, dragging effects, displacements of mirrors, decreases in the speed of light, distance intervals and time intervals of light propagation, measurements of time coordinates, and mathematical calculations of the same, and many absolute expectations were based on one completely false and impossible assumption: the existence of a material substance called ether.
Since we now know that the concept of ether (stationary, dragged along, or otherwise) was only a manmade myth and does not exist, therefore the absolute place or position from which all of these theories, measurements, and computations were made or described also does not exist. In reality, all of these illusionary theories, “measurements,” “computations,” and expectations were made with respect to “nothing. As George Gamow stated in his 1961 book, “One cannot move with respect to nothing…one can speak only about the relative motion of a material body in respect to another [material body].” It also follows that one also cannot measure, describe, or calculate something with respect to nothing. In this regard, let us also quote from Richard Feynman,
“You can only define what you can measure! Since it is self-evident that one cannot measure a velocity without seeing what he is measuring it relative to, therefore it is clear that there is no meaning to absolute velocity. The physicists should have realized that they can talk only about what they can measure.”
These were the fundamental theoretical reasons why Michelson could not detect a greater distance/time interval for light to propagate in the absolute direction of the Earth’s solar orbital motion through space, or in any other absolute direction of the Earth’s motion through space. There was never anything to detect! Such a greater or increasing distance/time interval for light to propagate in any direction with respect to nothing simply does not exist. It was yet another ether myth. It is also self-evident that Michelson, Morley, Kennedy, Thorndike, and anyone else cannot detect (by any method) a time interval difference that does not exist. Their elaborate efforts to do so were always an absolutely meaningless mission impossible!
There was also another related theoretical problem: Michelson’s experiments, the Kennedy-Thorndike experiments, repetitions thereof, and similar experiments were always assumed, described, interpreted, and believed to have resulted in “null results,” because completely different results were absolutely expected. However, all of these so-called null results actually resulted in empirically positive results, again because there was nothing to detect.
There was no difference in “time intervals for light propagation through ether or space,” that could be detected. There was no greater distance or time interval for light to propagate between relatively stationary mirrors in any direction of the Earth’s motion through ether or space that could be detected. There was no decrease in the velocity of light in the direction of the Earth’s motion through ether that could be detected. There was no displacement of mirrors from a propagating light ray in the direction of the Earth’s solar orbital motion, through the ether that could be detected. The reason for all of these factors is that there is no such thing as stationary ether, ether wind, or dragged along ether which could be detected either.
The scientific community simply refused to believe in all of these empirical results, and it still does. There is a huge lesson to be learned from these unscientific facts. That is: always believe in and trust reasonable physical observations and empirical results over illogical theoretical expectations, unobserved theoretical phenomena, and over mathematical theories, equations and computations.
The real reason why there was no change in the velocity of light in any direction of the Earth’s motion through space is because the light rays propagating in Michelson’s and Kennedy’s experiments always propagated through the same medium: clear air. It is well known from the Index of Refraction that light always propagates through clear air at sea level at almost velocity c (only 0.0003 less fast). This is also the real reason why light was always detected to be c in every light experiment conducted in any inertial frame of reference on Earth, or in space.
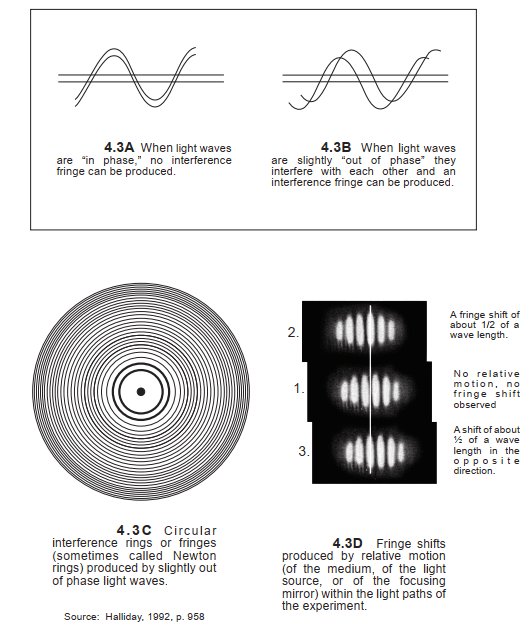
The next real reason for Michelson’s null results is physical and empirical. Let us postulate that the finite physical distance between two relatively stationary physical points (A and B) does not change just because such two points move in-tandem through space in any particular direction. Such finite distance between A and B always retains the same finite magnitude101 (Picture 1). The positive empirical results of Michelson’s and Kennedy’s experiments described this postulate, because no fringe shift was ever detected during either experiment.
In addition, let us also postulate that a light ray can only propagate at the constant velocity of c over any finite physical distance through the vacuum of space (or air), and that the velocity of such light ray at c does not change just because it propagates through the vacuum of space (or air) in any particular direction102 (Picture 1). The positive empirical results of Michelson’s and Kennedy’s experiments also described this postulate, because no fringe shift was ever detected during either experiment.
Picture 1: Light Measured At Velocity c To And From On Two Different Reference Frames
The fundamental reason for the last above postulate is because the medium (i.e. the vacuum or the air) through which the light ray is transmitting in Picture 1, is the primary determining factor for the velocity of the propagating light ray, and the medium never changed in either experiment. Light always transmits through a vacuum at the constant velocity of c (300,000 km/s, the fastest speed that nature allows), because there are no particles of matter in a perfect vacuum to slow light down or change its direction of transmission.
The velocity of the vehicle in which the light experiment is traveling has nothing to do with the velocity of the light ray within the vehicle. For example, if one of the vehicles in Picture 1 was filled with water the light ray would propagate much slower in that vehicle (about 225,000 km/s). The confirmation of these facts is the empirical index of refraction where light propagates at different velocities through different media.
Because of these above described postulates, there can never be an increasing physical distance or a greater time interval for light to propagate between two relatively stationary physical points (A and B), regardless of their in-tandem motion through the vacuum of empty space in any direction. Therefore, these postulates demonstrate the empirical validity of Michelson’s and Kennedy’s results. There never was a greater time interval for light to propagate within Michelson’s or Kennedy’s apparatus in any direction. These results have been demonstrated many times in many different reference frames.
Another real, physical and empirical reason for Michelson’s so-called null results, which apparently has been completely overlooked by everyone, was that M & M were actually only attempting to measure (or compare) one slightly out-of-phase light wave relative to another slightly out-of-phase light wave (Picture 2). Such out-of-phase light waves created an interference fringe when Michelson slightly changed the distance of one mirror by fine tuning its micrometer screw. M & M then assumed that the solar orbital motion of the Earth would change the distance/time interval which one light wave would have to propagate away from the ether. But, to paraphrase Feynman, one can only assume that which one can measure, and one can only measure that which one can see. One cannot measure unobserved or undetectable phenomena.
Picture 2: Out Of Phase Light Waves Can Create An Interference Fringe, And Relative Motion Within The Light Paths Of The Experiment Can Create Fringe Shifts
Regardless of what M & M were assuming, and regardless of the direction that their apparatus might be pointing in, if the finite physical distance of each arm of his apparatus always remained the same, there could never physically be an interference fringe shift: that is, a change of the relative phase positions of such out-of-phase light waves. Stated somewhat differently: As long as the physical length of each arm did not change (whatever its magnitude of distance might be), the relative phase position of each out-of-phase light wave would physically have to remain the same. This was the empirical result of the 1932 Kennedy-Thorndike experiment where one arm was intentionally constructed much shorter in length than the other arm (Picture 3). Therefore, the specific finite length of each arm and the specific finite distance that each light ray propagated in any direction were always irrelevant to the occurrence of a fringe shift.
Picture 3: The 1932 Kennedy-Thorndike Experiment
For all of the above real, physical and empirical reasons, a fringe shift could never physically occur when Michelson or Kennedy pointed the arms of his apparatus in different directions over a period of several months. Michelson’s and Kennedy’s attempts to detect an interference fringe shift, or a difference in time intervals for light propagation in any direction, were always a mission impossible. In order to visualize what actually happened in Michelson’s experiments, refer to Picture 4.
Picture 4: Two Perpendicular Light Pencils Propagating Within Michelson’s Apparatus At 4 Different Times, In The Absence Of Stationary Ether
The next real reasons for Michelson’s null results are technical. We have already described one of these technical reasons. If the arms of Michelson’s and Kennedy’s experiments always remained the same finite length, then a fringe shift (a change in the relative phase position of two slightly out-of-phase light waves) never could have physically occurred (Pictures 3 and 5). The only way that a fringe shift could have occurred would be if Michelson or Kennedy would have slightly adjusted the distance of the focusing mirror with the micrometer screw in order to obtain a fringe (Picture 6). But since both scientists already had obtained an interference fringe, there was no reason for them to obtain another one. And they never did.
Picture 5: Michelson’s Interference of Light Experiments
Picture 6: What Happened When Michelson Adjusted The Distance Of One Mirror In The Path Of One Light Pencil?
A second technical reason was because M & M’s apparatus was located in the concrete basement of a building (with no windows) so that its sensitive instruments would not be affected by traffic, heat, sunlight, etc. If M & M had desired to visually detect the motion of the Earth’s solar orbital motion, or any other relative motion of the Earth, they could have mounted a 10-inch telescope on the roof of the building and observed the light paths of a passing luminous planet (i.e. Venus) or a luminous planet that the Earth was passing (i.e. Mars, Jupiter, or Saturn) through the lens of the telescope and calculated the solar orbital motion of the Earth over a period of months.
However, the solar orbital motion of the Earth could never be detected by the interference method employed by M & M or Kennedy & Thorndike from the basement of a building, because (unlike the telescope) there never was any material body which moved within the light paths of their interference experiment, which technically could be detected by any method. The only motion which occurred within the light paths of their experiments was when the focusing mirror was adjusted by the micrometer screw to create an interference fringe. For this simple technical reason, none of these scientists could ever detect anything else, and none of them ever did.
Source: The Michelson-Morley paradox solved (You can also read the whole treatise there)
The Experiment of Fizeau
The short description of the experiment of Fizeau:
1. When the water is not moving in each tube, the light propagating through each tube has the same velocity, so the light waves in the two pencils of light that reach the eye are in phase.
2. When light propagates through water moving in different directions at 7 m/s, the velocity of light relative to the tube increases in the direction of flow A and decreases in the opposite direction of flow B. Thus the light waves propagating through tube A will arrive at the eye sooner (and in less time) than the light waves propagating through tube B. This causes an out of phase interference of the crests and troughs of such light waves which is visible to the eye as a pattern of interference fringes. The distance between each dark fringe is one wave length.
Picture 1: The experiment of Fizeau which determined the velocity of light in a moving liquid
When the flow of the water in the tubes is reversed, the pattern of interference fringes shifts, and the measurable magnitude of this shift can be computed to determine the difference in the velocity of light propagating relative to each tube.
Maxwell’s 1879 Ether Assumptions
Picture 1: Light propagating in any direction on the theoretically stationary Earth
The Picture 1 also illustrates Michelson’s theoretical distance and time interval (T1) for light to propagate in the direction perpendicular to the Earth’s solar orbital motion.
Picture 2: Light propagating in the direction of Earth’s absolute solar orbital motion and away from the stationary ether
The Picture 2 also illustrates the theoretical in-tandem displacement of mirrors A and B with respect to the stationary ether. Because empirically there is no ether, these theoretical displacements from ether cannot occur.
The light source, the beam splitter (BS) and the mirror M are affixed to the surface of the Earth at a finite distance apart, and for purposes of illustration we assume that they move in tandem to the right at 50% of c relative to the stationary ether and the Sun theoretically at rest in the ether. A light ray leaves the terrestrial light source at some point A0 and transmits at 100% of c toward the mirror at some point M0. During such propagation, the mirror theoretically displaces from point M0 to some point M1 due to such absolute solar orbital velocity with respect to the stationary ether. The light ray contacts the mirror at point M1 after traveling (from A0 to M1). The light ray then reflects from the mirror at M1 and begins to propagate back toward the light source. During such propagation, the material light source theoretically displaces from point A0 to some point A1 and then to some point A2.
When the light ray returns to the light source at point A2 the light ray has traveled a total distance/time interval while the light source and the mirrors have theoretically displaced in-tandem 1/2 of the total distance, an increase of 1/4 of the total distance because of the theoretical displacement. These were also Einstein’s computations for a greater distance/time interval of light propagation, which he referred to in Relativity at pp. 58 - 59. On the other hand, if there had been no motion of the Earth in an absolute direction(and thus no absolute displacement), then the light ray would only have traveled a total distance/time interval of 3/4 of the total distance. Strangely enough is what actually happened, because there is no ether and there can be no physical displacement from something that does not exist.
Astable Oscillator Circuit with 555 Timer
As we already analyze one simple Astable circuit with 555 Timer, now we will analyze one improved circuit with the same 555 timer. The oscillator circuit is shown on Picture 1. The main difference in this circuit is that resistor R3 now is connected to the trigger pin of the 555 timer and to the output of the circuit via the capacitor C3.
Picture 1: Astable oscillator circuit with 555 Timer
Time-domain analysis
The results of the transient analysis for this circuit in time domain is shown on Picture 2. These results are for the configuration of the circuit as shown on Picture 1. The power supply voltage is Vcc = 5 V DC. Resistor R3 = 270 Ω, R1 = R2 = 500 Ω, while the capacitors are C1 = 100 nF and C2 = C3 = 1 nF. As measured in the simulation, the frequency of the output signal is about f = 1.826 MHz.
Picture 2: Transient analysis - output voltage Vo wave form (time-domain)
The frequency of the output signal of this circuit can be changed, if we change the values of the components of the circuit. For example, we run simulations with three different values for resistors R1 and R2, and we got these results:
>> For R1 = R2 = 500 Ω -> f = 1.826 MHz;
>> For R1 = R2 = 820 Ω -> f = 1.662 MHz;
>> For R1 = R2 = 1 KΩ -> f = 1.632 MHz;
Just to notice here, the model of the NE555 timer circuit used in these simulations is idealised. In practice, this circuit has some upper limit for frequency of operation. This limit depends on the model and technology of the manufactured circuit. Usually, the older circuits had limit below 1 MHz, but the newer 555 Timers can have upper limit frequency of few MHz-s. Above the upper limit the circuit will be unstable.
Modulators and Feedback
There are numerous modulators, and here it is not objective to give an extensive overview, only the basic topologies are discussed.
PDM modulators
PDM modulators have resulted from the digital signal processing domain. In more and more equipment, the signal is available in digital form. For a switching amplifier it must be converted into a 1 bit signal at a high frequency. Sometimes, as with DSD audio data, this is even the native format. The output stage acts as a 1 bit D/A converter. Because the length of each bit is constant, and only the presence or non-presence of a bit is controlled, this is called Pulse Density Modulation (PDM). To convert a multi-bit signal to a 1-bit signal, oversampled noise shaping is used. Picture 1 shows a general noise shaper.
Picture 1: Noise shaper
The input signal Bin(z) has a larger number of bits than Bout(z). (When the input signal is analogue, a similar structure in the analogue domain constitutes a sigma-delta modulator). The block called "Quantizer" reduces the number of bits by simply passing only the most significant bits to Bout(z). The least significant bits, which are the error, are added to the input after passing through a transfer function J(z). It is easy to calculate Bout:
Bout(z) = Bin(z) - ε(z)(1 - J(z))
Suppose J(z) = z-1, one clock delay. The system is now a first-order noise shaper. Bin(z) is a 16 bit signal at 256fs and Bout is a 1 bit signal at 256fs. In that case, the quantizer transfers 1 bit to the output. The other 15 bits are the error signal. Bout equals:
Bout(z) = Bin(z) - ε(z)(1 - z^-1)
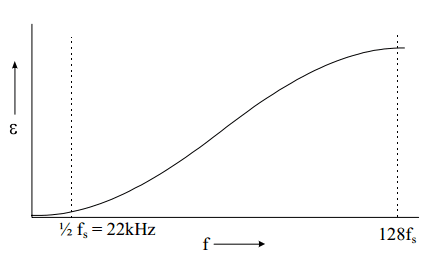
With z = e^( 2πj(f/256fs)), we see that for low frequencies (audio) the error in the output signal approaches zero. The error reaches a maximum for f = 128fs. See Picture 2.
Picture 2: Noise distribution as a function of frequency
Applying Bout to a 1 bit D/A converter and filtering above 20 kHz reconstructs the original signal. In the time domain such a noise shaper is a way to convert resolution in the amplitude domain to resolution in the time domain. It outputs bits at high speed in such a way that the average is the intended output (which has a higher amplitude resolution). This way it is also easy to see that although the D/A converter is only 1 bit, it should have a 16 bit accuracy.
To convert the audio signal to 256fs, an oversampling interpolating filter must proceed the noise shaper. A two times oversampling filter works as follows. Suppose the spectrum of the signal sampled at fs looks like Picture 3. This signal is converted to a sampling frequency of 2fs by inserting a sample of value zero after every original sample. See Picture 4. Because every sample is a Dirac pulse of proportional height, the frequency spectrum stays exactly the same.
Picture 3: Spectrum of the signal
Picture 4: Inserting zero samples
Next, the signal is applied to a digital filter at 2fs that filters out the middle replica, see Picture 5. After that, the frequency spectrum of the signal looks exactly like it has been sampled at 2fs. These techniques, oversampling interpolating filtering and noise shaping are essential for all digital PDM systems, although the exact realisation may vary.
Picture 5: Filtering out the middle replica
Assume, the 256 times oversampling for a CD player D/A converter is done in two stages. A four times oversampling filter is followed by a 64 times linear interpolator. The direct use of a 256 times oversampling filter is also possible, but the filter would be very large. A linearly interpolating filter is easier to build, and at 4fs the distortion that it creates has only little effect in the audio band. Then, at 256fs, a second order noise shaper suffices to get a 1 bit signal with 16 bit resolution in the audio band. Unfortunately 256fs = 11MHz which is too high for power switching.
Another possibility is to use only 32fs with an eighth order noise shaper.
Noise shapers with a higher order than three are prone to instability, and it is necessary to manipulate the system when it becomes potentially unstable. Extensive simulations are necessary for evaluation. Even in this case, the switching frequency is 1.4 MHz. The high switching frequencies are a general problem of PDM modulators. Bit-flipping techniques can reduce the average frequency at which the output changes somewhat.
Digital PWM modulators
Digital PWM modulators offer a lower switching frequency than PDM modulators. The Pulse Amplitude Modulated (PAM) samples are converted to PWM. This could be done by giving each pulse a length that is proportional to the original amplitude. However, for CD quality the internal clock frequency would have
to be 2^16 * 44.1 kHz = 2.9 GHz, which is way too high. Furthermore, the frequency spectrum of the PWM signal would not equal that of the PAM signal. This can be calculated, but for a better understanding it is best to realise that natural sampling yields the best results because it does not introduce harmonic distortion. In natural sampling, the audio signal is compared to a triangle or sawtooth waveform (more details below). When we convert a digital PAM signal directly to PWM, it looks as if, looking in the analogue domain, we compared the sawtooth waveform to a step-like representation of the signal instead of the signal itself. This is called uniform sampling. See Picture 6. It introduces harmonic distortion, which depends on many factors including the signal frequency, the switching frequency and the modulation depth.
Picture 6: Natural sampling versus uniform sampling
To approximate natural sampling, linear or higher order interpolation between two or more samples is used to approach the natural PWM pulse width. When the pulse width has been calculated, the sample instant can be the beginning or the end of the pulse (single sided modulation) or the middle (double sided modulation). There are more aspects that deserve attention, but a full discussion of these would be beyond the scope of this article.
Analogue PWM modulators
In the analogue domain a PWM signal can be generated by comparing the audio signal to a triangle or sawtooth waveform. This technique, called natural sampling, is the basis of almost all analogue modulators. See Picture 7. When the momentary value of the input signal is larger than the triangle, the output of the switch is high. It is easy to see that in this way the pulse width at the output is proportional to the input voltage. The modulator does not introduce harmonic distortion, only (multiples of) the carrier frequency and (multiples of) harmonics of the modulating frequency around the carrier.
Picture 7: Open-loop class D modulator
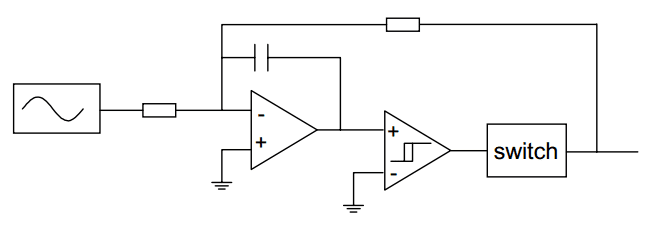
The main problem is the lack of feedback. Output stage inaccuracies, nonlinearities, timing errors and supply voltage variations all contribute to the distortion. We will discuss feedback here, as it is so closely related to the modulator. Picture 8 shows a modulator with feedback. Both inputs to the comparator have triangular waveforms. Picture 9 shows the waveforms for zero and positive output voltage. At zero output voltage, the feedback signal intercepts the reference triangle in such a way that the duty cycle is 50 %. When the output voltage is not zero, the rising and falling slope of the feedback triangle are different, leading to a larger (or smaller) duty cycle.
Picture 8: Modulator with feedback
Picture 9: Signals at the input of the comparator of the feedback modulator
The slew rate of the feedback signal must always be smaller than the slew rate of the reference triangle. Otherwise, the amplifier starts oscillating at a very high frequency. This constitutes a compromise between switching frequency and loop gain. The slew rate requirement can roughly be translated to the demand that the loop gain of the amplifier at the switching frequency is smaller than 0.5. Thanks to the integrator, the open loop frequency transfer of the amplifier is first order, so that the loop gain at a certain frequency has a maximum that is related to the switching frequency. A way to get more loop gain at low (audio) frequencies is by introducing a range with second order frequency response in the loop. As long as the loop gain is back to first order at 0 dB, stability is ensured. This can be done in the modulator by adding a second integrator before the comparator while bypassing it for high frequencies. In practical realisations of a feedback modulator, the triangle is generated by adding a square wave to the input of the integrator. The feedback properties of this type of modulator can also be used when the input signal is generated by a digital modulator. Because in that case the bitstream is already clocked, the negative input of the comparator can be tied to ground. Other techniques, like the one cycle control technique or pulse edge delay error correction, are similar to this modulator in their attempt to control the integral of the switched output voltage.
The high frequency oscillation that occurs in a feedback modulator when the feedback signal is too large, is exploited in the self-oscillating class D modulator. See Picture 10. The comparator is equipped with some hysteresis to control the switching frequency. Other factors that influence the switching frequency are the integrator time constant and the output voltage. For large output voltages, the frequency approaches zero. This can cause aliasing problems that can be overcome by using a comparator with a variable hysteresis dependent on the input voltage. In that way the oscillator frequency is kept constant over a wide range of output voltages.
Picture 10: Self oscillating class D modulator
In the situations above, feedback is successfully taken before the output filter. The combination with feedback after the filter is more troublesome.
Subscribe to:
Posts (Atom)