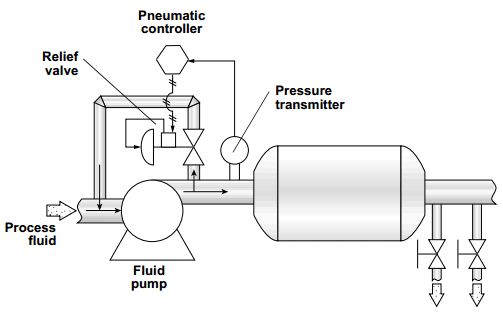
Multi-Variable / Advanced Control Loops

Multivariable loops are control loops in which a primary controller controls one process variable by sending signals to a controller of a different loop that impacts the process variable of the primary loop. For example, the primary process variable may be the temperature of the fluid in a tank that is heated by a steam jacket (a pressurized steam chamber surrounding the tank). To control the primary variable (temperature), the primary (master) controller signals the secondary (slave) controller that is controlling steam pressure. The primary controller will manipulate the setpoint of the secondary controller to maintain the setpoint temperature of the primary process variable (Picture 1).

Picture 1: Multivariable Loop


When tuning a control loop, it is important to take into account the presence of multivariable loops. The standard procedure is to tune the secondary loop before tuning the primary loop because adjustments to the secondary loop impact the primary loop. Tuning the primary loop will not impact the secondary loop tuning.

Feedforward Control

Feedforward control is a control system that anticipates load disturbances and controls them before they can impact the process variable. For feedforward control to work, the user must have a mathematical understanding of how the manipulated variables will impact the process variable. Picture 2 shows a feedforward loop in which a flow transmitter opens or closes a hot steam valve based on how much cold fluid passes through the flow sensor.

Picture 2: Feedforward Control


An advantage of feedforward control is that error is prevented, rather than corrected. However, it is difficult to account for all possible load disturbances in a system through feedforward control. Factors such as outside temperature, buildup in pipes, consistency of raw materials, humidity, and moisture content can all become load disturbances and cannot always be effectively accounted for in a feedforward system. In general, feedforward systems should be used in cases where the controlled variable has the potential of being a major load disturbance on the process variable ultimately being controlled. The added complexity and expense of feedforward control may not be equal to the benefits of increased control in the case of a variable that causes only a small load disturbance.

Feedforward Plus Feedback Control

Because of the difficulty of accounting for every possible load disturbance in a feedforward system, feedforward systems are often combined with feedback systems. Controllers with summing functions are used in these combined systems to total the input from both the feedforward loop and the feedback loop, and send a unified signal to the final control element. Picture 3 shows a feedforward-plus-feedback loop in which both a flow transmitter and a temperature transmitter provide information for controlling a hot steam valve.

Picture 3: Feedforward Plus Feedback Control System



This article has discussed specific types of control loops, what components are used in them, and some of the applications (e.g., flow, pressure, temperature) they are applied to. In practice, however, many independent and interconnected loops are combined to control the workings of a typical plant. This section will acquaint you with some of the methods of control currently being used in process industries.

Cascade Control

Cascade control is a control system in which a secondary (slave) control loop is set up to control a variable that is a major source of load disturbance for another primary (master) control loop. The controller of the primary loop determines the setpoint of the summing controller in the secondary loop (Picture 4).

Picture 4: Cascade Control

Batch Control

Batch processes are those processes that are taken from start to finish in batches. For example, mixing the ingredients for a juice drinks is often a batch process. Typically, a limited amount of one flavor (e.g. orange drink or apple drink) is mixed at a time. For these reasons, it is not practical to have a continuous process running. Batch processes often involve getting the correct proportion of ingredients into the batch. Level, flow, pressure, temperature, and often mass measurements are used at various stages of batch processes. A disadvantage of batch control is that the process must be frequently restarted. Start-up presents control problems because, typically, all measurements in the system are below setpoint at start-up. Another disadvantage is that as recipes change, control instruments may need to be re-calibrated.

Ratio Control

Imagine a process in which an acid must be diluted with water in the proportion two parts water to one part acid. If a tank has an acid supply on one side of a mixing vessel and a water supply on the other, a control system could be developed to control the ratio of acid to water, even though the water supply itself may not be controlled. This type of control system is called ratio control (Picture 5). Ratio control is used in many applications and involves a contoller that receives input from a flow measurement device on the unregulated (wild) flow. The controller performs a ratio calculation and signals the appropriate setpoint to another controller that sets the flow of the second fluid so that the proper proportion of the second fluid can be added.

Picture 5: Ratio Control

Ratio control might be used where a continuous process is going on and an additive is being put into the flow (e.g., chlorination of water).

Selective Control

Selective control refers to a control system in which the more important of two variables will be maintained. For example, in a boiler control system, if fuel flow outpaces air flow, then uncombusted fuel can build up in the boiler and cause an explosion. Selective control is used to allow for an air-rich mixture, but never a fuel-rich mixture. Selective control is most often used when equipment must be protected or safety maintained, even at the cost of not maintaining an optimal process variable setpoint.

Fuzzy Control

Fuzzy control is a form of adaptive control in which the controller uses fuzzy logic to make decisions about adjusting the process. Fuzzy logic is a form of computer logic where whether something is or is not included in a set is based on a grading scale in which multiple factors are accounted for and rated by the computer. The essential idea of fuzzy control is to create a kind of artificial intelligence that will account for numerous variables, formulate a theory of how to make improvements, adjust the process, and learn from the result.
Fuzzy control is a relatively new technology. Because a machine makes process control changes without consulting humans, fuzzy control removes from operators some of the ability, but none of the responsibility, to control a process.

Process Control Loops

This article is about how control components and control algorithms are integrated to create a process control system. Because in some processes many variables must be controlled, and each variable can have an impact on the entire system, control systems must be designed to respond to disturbances at any point in the system and to mitigate the effect of those disturbances throughout the system.

Single Control Loops

Control loops can be divided into two categories: Single variable loops and multi-variable loops.

Feedback Control

A feedback loop measures a process variable and sends the measurement to a controller for comparison to setpoint. If the process variable is not at setpoint, control action is taken to return the process variable to setpoint. Picture 1 illustrates a feedback loop in which a transmitter measures the temperature of a fluid and, if necessary, opens or closes a hot steam valve to adjust the fluid’s temperature.

Picture 1: Feedback Loop


An everyday example of a feedback loop is the cruise control system in an automobile. A setpoint is established for speed. When the car begins to climb a hill, the speed drops below setpoint and the controller adjusts the throttle to return the car’s speed to setpoint. Feedback loops are commonly used in the process control industry. The advantage of a feedback loop is that it directly controls the desired process variable. The disadvantage to feedback loops is that the process variable must leave setpoint for action to be taken.

Examples of Single Control Loops

While each application has its own characteristics, some general statements can be made about pressure, flow, level, and temperature loops.

Pressure Control Loops

Pressure control loops vary in speed—that is, they can respond to changes in load or to control action slowly or quickly. The speed required in a pressure control loop may be dictated by the volume of the process fluid. High-volume systems (e.g., large natural gas storage facilities) tend to change more slowly than low-volume systems (Picture 2).

Picture 2: A Pressure Loop

Flow Control Loops

Generally, flow control loops are regarded as fast loops that respond to changes quickly. Therefore, flow control equipment must have fast sampling and response times. Because flow transmitters tend to be rather sensitive devices, they can produce rapid fluctuations or noise in the control signal. To compensate for noise, many flow transmitters have a damping function that filters out noise. Sometimes, filters are added between the transmitter and the control system. Because the temperature of the process fluid affects its density, temperature measurements are often taken with flow measurements and compensation for temperature is accounted for in the flow calculation. Typically, a flow sensor, a transmitter, a controller, and a valve or pump are used in flow control loops (Picture 3).

Picture 3: A Flow Loop

Level Control Loops

The speed of changes in a level control loop largely depends on the size and shape of the process vessel (e.g., larger vessels take longer to fill than smaller ones) and the flow rate of the input and outflow pipes. Manufacturers may use one of many different measurement technologies to determine level, including radar, ultrasonic, float gauge, and pressure measurement. The final control element in a level control loop is usually a valve on the input and/or outflow connections to the tank (Picture 4). Because it is often critical to avoid tank overflow, redundant level control systems are sometimes employed.

Picture 4: A Level Loop

Temperature Control Loops

Because of the time required to change the temperature of a process fluid, temperature loops tend to be relatively slow. Feedforward control strategies are often used to increase the speed of the temperature loop response. RTDs or thermocouples are typical temperature sensors. Temperature transmitters and controllers are used, although it is not uncommon to see temperature sensors wired directly to the input interface of a controller. The final control element for a temperature loop is usually the fuel valve to a burner or a valve to some kind of heat exchanger. Sometimes, cool process fluid is added to the mix to maintain temperature (Picture 5).

Picture 5: A Temperature Loop

Proportional, PI, and PID Control (Algorithms)

By using all three control algorithms together, process operators can:

❑ Achieve rapid response to major disturbances with derivative control;
❑ Hold the process near setpoint without major fluctuations with proportional control;
❑ Eliminate offset with integral control.


Not every process requires a full PID control strategy. If a small offset has no impact on the process, then proportional control alone may be sufficient.
PI control is used where no offset can be tolerated, where noise (temporary error readings that do not reflect the true process variable condition) may be present, and where excessive dead time (time after a disturbance before control action takes place) is not a problem. In processes where no offset can be tolerated, no noise is present, and where dead time is an issue, customers can use full PID control. The Table on Picture 1 shows common types of control loops and which types of control algorithms are typically used.

Picture 1: Control Loops and Control Algorithms Table

Tuning of Controllers

Controllers are tuned in an effort to match the characteristics of the control equipment to the process so that two goals are achieved:

❑ The system responds quickly to errors;
❑ The system remains stable (PV does not oscillate around the SP).

Gain

Controller tuning is performed to adjust the manner in which a control valve (or other final control element) responds to a change in error. In particular, we are interested in adjusting the gain of the controller such that a change in controller input will result in a change in controller output that will, in turn, cause sufficient change in valve position to eliminate error, but not so great a change as to cause instability or cycling.

Gain is defined simply as the change in output divided by the change in input.

Examples:

Change in Input to Controller - 10%
Change in Controller Output - 20%
Gain = 20% / 10% = 2

Change in Input to Controller - 10%
Change in Controller Output - 5%
Gain = 5% / 10% = 0.5

Gain Plot - The Picture 1 below is simply another graphical way of representing the concept of gain.

Picture 1: Graphical Representation of Gain Concept

Proportional Mode

The proportional mode is used to set the basic gain value of the controller. The setting for the proportional mode may be expressed as either:

1. Proportional Gain
2. Proportional Band

Proportional Gain

In electronic controllers, proportional action is typically expressed as proportional gain. Proportional Gain (Kc) answers the question: "What is the percentage change of the controller output relative to the percentage change in controller input?" Proportional Gain is expressed as:

Gain Kc = ∆Output[%] / ∆Input[%]

Proportional Band

Proportional Band (PB) is another way of representing the same information and answers this question: "What percentage of change of the controller input span will cause a 100% change in controller output?" Proportional Band is expressed as:

PB = ∆Input (% Span) For 100% ∆Output

Converting Between PB and Gain

A simple equation converts gain to proportional Band:

PB = 100/Gain

Also recall that:

Gain = 100%/PB


Picture 2 shows the relationship between proportional gain and proportional band.

Picture 2: Relationship of Proportional Gain and Proportional Band

Limits of proportional action

>> Responds Only to a Change in error - Proportional action responds only to a change in the magnitude of the error.
>> Does Not Return the PV to Setpoint - Proportional action will not return the PV to setpoint. It will, however, return the PV to a value that is within a defined span (PB) around the PV.

Proportional Action - Closed Loop

Loop Gain - Every loop has a critical or natural frequency. This is the frequency at which cycling may exist. This critical frequency is determined by all of the loop components. If the loop gain is too high at this frequency, the PV will cycle around the SP; i.e. the process will become unstable.

Proportional Summary

For the proportional mode, controller output is a function of a change in error. Proportional band is expressed in terms of the percentage change in error that will cause 100% change in controller output. Proportional gain is expressed as the percentage change in output divided by the percentage change in input.

PB = (∆Input, % / ∆Output, % ) x 100 = 100/Gain

∆ Controller Output = (Change in Error)(Gain)

1. Proportional Mode responds only to a change in error;
2. Proportional mode alone will not return the PV to SP.

Advantages - Simple.
Disadvantages - Error.

Settings - PB settings have the following effects:

>> Small PB (%) Minimize Offset;
>> High Gain (%) Possible cycling;
>> Large PB (%) Large Offset;
>> Low Gain Stable Loop.

Tuning - reduce PB (increase gain) until the process cycles following a disturbance, then double the PB (reduce gain by 50%).

Integral Mode

Duration of Error and Integral Mode - Another component of error is the duration of the error, i.e., how long has the error existed? The controller output from the integral or reset mode is a function of the duration of the error.

Open Loop Analysis

The purpose of integral action is to return the PV to SP. This is accomplished by repeating the action of the proportional mode as long as an error exists. With the exception of some electronic controllers, the integral or reset mode is always used with the proportional mode.

Integral, or reset action, may be expressed in terms of:

>> Repeats Per Minute - How many times the proportional action is repeated each minute;
>> Minutes Per Repeat - How many minutes are required for 1 repeat to occur.

Closed Loop Analysis

Closed Loop With Reset - Adding reset to the controller adds one more gain component to the loop. The faster the reset action, the greater the gain.

Slow Reset Example - In this example the loop is stable because the total loop gain is not too high at the loop critical frequency (Picture 3). Notice that the process variable does reach set point due to the reset action.

Picture 3: Slow Reset - Closed Loop


Fast Reset Example - In the example the rest is too fast and the PV is cycling around the SP (Picture 4).

Picture 4: Fast Reset - Closed Loop

Reset Windup

Reset windup is described as a situation where the controller output is driven from a desired output level because of a large difference between the set point and the process variable (Picture 5).

Picture 5: Reset Windup - Anti-Reset Windup


Shutdown - Reset windup is common on shut down because the process variable may go to zero but the set point has not changed, therefore this large error will drive the output to one extreme.
Startup - At start up, large process variable overshoot may occur because the reset speed prevents the output from reaching its desired value fast enough (Picture 6).

Picture 6: Reset Windup - Shutdown and Startup


Anti Reset Windup - Controllers can be modified with an anti-reset windup (ARW) device. The purpose of an anti-reset option is to allow the output to reach its desired value quicker, therefore minimizing the overshoot.

Integral (Reset) Summary

Output is a repeat of the proportional action as long as error exists. The units are in terms of repeats per minute or minutes per repeat.

Advantages - Eliminates error.
Disadvantages - Reset windup and possible overshoot.

Fast Reset (Large Repeats/Min.,Small Min./Repeat):

1.High Gain;
2.Fast Return To Setpoint;
3.Possible Cycling.

Slow Reset (Small Repeats/Min.,Large Min./Repeats):

1.Low Gain;
2.Slow Return To Setpoint;
3.Stable Loop.

Trailing and Error Tuning - Increase repeats per minute until the PV cycles following a disturbance, then slow the reset action to a value that is 1/3 of the initial setting.

Derivative Mode

Some large and/or slow process do not respond well to small changes in controller output. For example, a large liquid level process or a large thermal process (a heat exchanger) may react very slowly to a small change in controller output. To improve response, a large initial change in controller output may be applied. This action is the role of the derivative mode.

The derivative action is initiated whenever there is a change in the rate of change of the error (the slope of the PV). The magnitude of the derivative action is determined by the setting of the derivative, the mode of a PID controller and the rate of change of the PV. The derivative setting is expressed in terms of minutes. In operation, the controller first compares the current PV with the last value of the PV. If there is a change in the slope of the PV, the controller determines what its output would be at a future point in time (the future point in time is determined by the value of the derivative setting, in minutes). The derivative mode immediately increases the output by that amount (Picture 7).

Picture 7: Derivative Action is based on the rate of change in Error (Y/X)

Example

Let's start a closed loop example by looking at a temperature control system. In this example, the time scale has been lengthened to help illustrate controller actions in a slow process. Assume a proportional band setting of 50%. There is no reset at this time. The proportional gain of 2 acting on a 10% change in set point results in a change in controller output of 20%. Because temperature is a slow process the setting time after a change in error is quite long. And, in this example, the PV never becomes equal to the SP because there is no reset.

Rate Effect - To illustrate the effect of rate action, we will add there a mode with a setting of 1 minute. Notice the very large controller output at time 0. The output spike is the result of rate action. Recall that the change in output due to rate action is a function of the speed (rate) of change of error, which in a step is nearly infinite. The addition of rate alone will not cause the process variable to match the set point (Picture 8).

Picture 8: No Rate, Small Rate examples, Closed Loop



Effect of Fast Rate - Let's now increase the rate setting to 10 minutes. The controller gain is now much higher. As a result, both the IVP (controller output) and the PV are cycling. The point here is that increasing the rate setting will not cause the PV to settle at the SP (Picture 9).

Picture 9: P+D, High Rate Setting, Closed Loop Analysis


Need for Reset Action - It is now clear that reset must be added to bring process variable back to set point.

Applications - Because this component of the controller output is dependent on the speed of change of the input or error, the output will be very erratic if rate is used on fast process or one with noisy signals. The controller output, as a result of rate, will have the greatest change when the input changes rapidly.

Controller Option to Ignore Change in SP - Many controllers, especially digital types, are designed to respond to changes in the PV only, and to ignore changes in SP. This feature eliminates a major upset that would occur following a change in the setpoint.

Derivative (Rate) Summary

Rate action is a function of the speed of change of the error. The units are minutes. The action is to apply an immediate response that is equal to the proportional plus reset action that would have occurred some number of minutes I the future.

Advantages - Rapid output reduces the time that is required to return PV to SP in slow process.
Disadvantage - Dramatically amplifies noisy signals; can cause cycling in fast processes.

Settings

Large (Minutes):

1.High Gain
2.Large Output Change
3.Possible Cycling

Small (Minutes):

1.Low Gain
2.Small Output Change
3.Stable Loop

Trial and Error Tuning - Increase the rate setting until the process cycles following a disturbance, then reduce the rate setting to one-third of the initial value.

Controller Algorithms and Tuning

In the previous articles of this category were described the purpose of control, defined individual elements within control loops, and demonstrated the symbology used to represent those elements in an engineering drawing. The examples of control loops used thus far have been very basic. In practice, control loops can be fairly complex. The strategies used to hold a process at setpoint are not always simple, and the interaction of numerous setpoints in an overall process control plan can be subtle and complex. In this article, you will be introduced to some of the strategies and methods used in complex process control loops. The goal of this article is to:

❑ Differentiate between discrete, multistep, and continuous controllers.
❑ Describe the general goal of controller tuning.
❑ Describe the basic mechanism, advantages and disadvantages of the following mode of controller action:
• Proportional action;
• Intergral action;
• Derivative action;
❑ Give examples of typical applications or situations in which each mode of controller action would be used.
❑ Identify the basic implementation of P, PI and PID control in the following types of loops:
• Pressure loop;
• Flow loop;
• Level loop;
• Temperature loop.

Controller Algorithms

The actions of controllers can be divided into groups based upon the functions of their control mechanism. Each type of controller has advantages and disadvantages and will meet the needs of different applications. Grouped by control mechanism function, the three types of controllers are:

❑ Discrete controllers
❑ Multistep controllers
❑ Continuous controllers

Discrete controllers

Discrete controllers are controllers that have only two modes or positions: on and off. A common example of a discrete controller is a home hot water heater. When the temperature of the water in the tank falls below setpoint, the burner turns on. When the water in the tank reaches setpoint, the burner turns off. Because the water starts cooling again when the burner turns off, it is only a matter of time before the cycle begins again. This type of control doesn’t actually hold the variable at setpoint, but keeps the variable within proximity of setpoint in what is known as a dead zone (Picture 1).

Picture 1: Discrete Control

Multistep controllers

Multistep controllers are controllers that have at least one other possible position in addition to on and off. Multistep controllers operate similarly to discrete controllers, but as setpoint is approached, the multistep controller takes intermediate steps. Therefore, the oscillation around setpoint can be less dramatic when multistep controllers are employed than when discrete controllers are used (Picture 2).

Picture 2: Multistep Control Profile

Continuous controllers

Controllers automatically compare the value of the PV to the SP to determine if an error exists. If there is an error, the controller adjusts its output according to the parameters that have been set in the controller.

Picture 3: Automatic Feedback Control


The tuning parameters essentially determine (Picture 3):

>> How much correction should be made? The magnitude of the correction (change in controller output) is determined by the proportional mode of the controller.
>> How long should the correction be applied? The duration of the adjustment to the controller output is determined by the integral mode of the controller.
>> How fast should the correction be applied? The speed at which a correction is made is determined by the derivative mode of the controller.

Mode of Operation of different Controller Types

This article explains the control response of various controller types and the significance of parameters. As in the explanation of controlled systems, the step response is used for this description. The input variable to the controller is the system deviation – that is, the difference between the desired value and the actual value of the controlled variable.

Proportional (P) controller

In the case of the proportional controller, the actuation signal is proportional to the system deviation. If the system deviation is large, the value of the manipulated variable is large. If the system deviation is small, the value of the manipulated variable is small. The time response of the P controller in the ideal state is exactly the same as the input variable (see Picture 1).

Picture 1: Time response of the P controller


The relationship of the manipulated variable to the system deviation is the proportional coefficient or the proportional gain. These are designated by xp, Kp or similar. These values can be set on a P controller. It determines how the manipulated variable is calculated from the system deviation. The proportional gain is calculated as:

Kp = y0 / x0


If the proportional gain is too high, the controller will undertake large changes of the manipulating element for slight deviations of the controlled variable. If the proportional gain is too small, the response of the controller will be too weak resulting in unsatisfactory control. A step in the system deviation will also result in a step in the output variable. The size of this step is dependent on the proportional gain. In practice, controllers often have a delay time, that is a change in the manipulated variable is not undertaken until a certain time has elapsed after a change in the system deviation. On electrical controllers, this delay time can normally be set. An important property of the P controller is that as a result of the rigid relationship between system deviation and manipulated variable, some system deviation always remains. The P controller cannot compensate this remaining system deviation.

Integral-action (I) controller

The I controller adds the system deviation over time. It integrates the system deviation. As a result, the rate of change (and not the value) of the manipulated variable is proportional to the system deviation. This is demonstrated by the step response of the I controller: if the system deviation suddenly increases, the manipulated variable increases continuously. The greater the system deviation, the steeper the increase in the manipulated variable (see Picture 2).

Picture 2: Time response of the I controller


For this reason the I controller is not suitable for totally compensating remaining system deviation. If the system deviation is large, the manipulated variable changes quickly. As a result, the system deviation becomes smaller and the manipulated variable changes more slowly until equilibrium is reached.
Nonetheless, a pure I controller is unsuitable for most controlled systems, as it either causes oscillation of the closed loop or it responds too slowly to system deviation in systems with a long time response. In practice there are hardly any pure I controllers.

PI controller

The PI controller combines the behaviour of the I controller and P controller. This allows the advantages of both controller types to be combined: fast reaction and compensation of remaining system deviation. For this reason, the PI controller can be used for a large number of controlled systems. In addition to proportional gain, the PI controller has a further characteristic value that indicates the behaviour of the I component: the reset time (integral-action time).

Picture 3: Time response of the PI Controller

Reset time

The reset time is a measure for how fast the controller resets the manipulated variable (in addition to the manipulated variable generated by
the P component) to compensate for a remaining system deviation. In other words: the reset time is the period by which the PI controller is faster than the pure I controller. Behaviour is shown by the time response curve of the PI controller (see Picture 3).

The reset time is a function of proportional gain Kp as the rate of change of the manipulated variable is faster for a greater gain. In the case of a long reset time, the effect of the integral component is small as the summation of the system deviation is slow. The effect of the integral component is large if the reset time is short. The effectiveness of the PI controller increases with increase in gain Kp and increase in the I-component (i.e., decrease in reset time). However, if these two values are too extreme, the controller’s intervention is too coarse and the entire control loop starts to oscillate. Response is then not stable. The point at which the oscillation begins is different for every controlled system and must be determined during commissioning.

PD controller

The PD controller consists of a combination of proportional action and differential action. The differential action describes the rate of change of the system deviation. The greater this rate of change – that is the size of the system deviation over a certain period – the greater the differential component. In addition to the control response of the pure P controller, large system deviations are met with very short but large responses. This is expressed by the derivative-action time (rate time).

Picture 4: Time response of the PD Controller

Derivative-action time

The derivative-action time Td is a measure for how much faster a PD controller compensates a change in the controlled variable than a pure P controller. A jump in the manipulated variable compensates a large part of the system deviation before a pure P controller would have reached this value. The P component therefore appears to respond earlier by a period equal to the rate time (see Picture 4).

Two disadvantages result in the PD controller seldom being used. Firstly, it cannot completely compensate remaining system deviations. Secondly, a slightly excessive D component leads quickly to instability of the control loop. The controlled system then tends to oscillate.

PID controller

In addition to the properties of the PI controller, the PID controller is complemented by the D component. This takes the rate of change of the system deviation into account. If the system deviation is large, the D component ensures a momentary extremely high change in the manipulated variable. While the influence of the D component falls of immediately, the influence of the I component increases slowly. If the change in system deviation is slight, the behaviour of the D component is negligible. This behaviour has the advantage of faster response and quicker compensation of system deviation in the event of changes or disturbance variables. The disadvantage is that the control loop is much more prone to oscillation and that setting is therefore more difficult. Picture 5 shows the time response of a PID controller.

Picture 5: Time response of the PID Controller

Derivative-action time

As a result of the D component, this controller type is faster than a P controller or a PI controller. This manifests itself in the derivative-action time Td. The derivative-action time is the period by which a PID controller is faster than the PI controller.

Controllers

The previous article Controlled System, dealt with the controlled system - the part of the system which is controlled by a controller. This article is about the controller. The controller is the device in a closed-loop control that compares the measured value (actual value) with the desired value, and then calculates and outputs the manipulated variable. The above section showed that controlled systems can have very different responses. There are systems which respond quickly, systems that respond very slowly and systems with storage property.
For each of these controlled systems, changes to the manipulated variable y must take place in a different way. For this reason there are various types of controller each with its own control response. The control engineer has the task of selecting the controller with the most suitable control response for the controlled system.

Control response

Control response is the way in which the controller derives the manipulated variable from the system deviation. There are two broad categories: continuous-action controllers and non-continuous-action controllers.

Continuous-action controller

The manipulated variable of the continuous-action controller changes continuously dependent on the system deviation. Controllers of this type give the value of the system deviation as a direct actuating signal to the manipulating element. An example of this type of controller is the centrifugal governor (Picture 1). It changes its moment of inertia dependent on speed, and thus has a direct influence on speed.

Picture 1: Centrifugal governor as Continuous-action controller

Non-continuous-action controller

The manipulated variable of a non-continuous-action controller can only be changed in set steps. The best-known non-continuous-action controller is the two-step control that can only assume the conditions "on" or "off". An example is the thermostat of an iron (Picture 2). It switches the electric current for the heating element on or off depending on the temperature.

Picture 2: Thermostat of an iron as Non-continuous-action controller

Time response of a controller

Every controlled system has its own time response. This time response depends on the design of the machine or system and cannot be influenced by the control engineer. The time response of the controlled system must be established through experiment or theoretical analysis. The controller is also a system and has its own time response. This time response is specified by the control engineer in order to achieve good control performance.

The time response of a continuous-action controller is determined by three components:

>> Proportional component (P component)
>> Integral component (I component)
>> Differential component (D component)

The above designations indicate how the manipulated variable is calculated from the system deviation.

Proportional controller

In the proportional controller, the manipulated variable output is proportional to the system deviation. If the system deviation is large, the value of the manipulated variable is large. If the system deviation is small, the value of the manipulated variable is small. As the manipulated variable is proportional to the system deviation, the manipulated variable is only present if there is a system deviation. For this reason, a proportional controller alone cannot achieve a system deviation of zero. In this case no manipulated variable will be present and there would therefore be no control. The output response of the proportional controller for proper input is shown on Picture 3.

Picture 3: Proportional Controller response (input and output)

Integral-action controller

An integral-action controller adds the system deviation over time, that is, it is integrated. For example, if a system deviation is constantly present, the value of the manipulated variable continues to increase as it is dependent on summation over time. However, as the value of the manipulated variable continues to increase, the system deviation decreases. This process continues until the system deviation is zero. Integral-action controllers or integral components in controllers are therefor used to avoid permanent system deviation. The output response of the integral-action controller is shown on Picture 4.

Picture 4: Integral-action Controller response (input and output)

Differential-action controller

The differential component evaluates the speed of change of the system deviation. This is also called differentiation of the system deviation. If the system deviation is changing fast, the manipulated variable is large. If the system deviation is small, the value of manipulated variable is small. The response of the differential-action controller is shown on Picture 5. A controller with D component alone does not make any sense, as a manipulated variable would only be present during change in the system deviation. A controller can consist of a single component, for example a P controller or an I controller. A controller can also be a combination of several components - the most common form of continuous-action controller is the PID controller.

Picture 5: Differential-action Controller response (input and output)

Technical details of controllers

In automation technology controllers are almost exclusively electrical or electronic. Although mechanical and pneumatic controllers are often shown as examples in text books, they are hardly ever found in modern systems. Electrical and electronic controllers work with electrical input and output signals. The transducers are sensors which convert physical variables into voltage or current. The manipulating elements and servo drives are operated by current or voltage outputs. Theoretically, there is no limit to the range of these signals. In practice, however, standard ranges have become established for controllers:

1. For voltage: 0 ... 10 V; -10 ... +10 V;
2. For current: 0 ... 20 mA; 4 ... 20 mA;

Internal processing of signals in the controller is either analog with operational amplifier circuits or digital with microprocessor systems:

>> In circuits with operational amplifiers, voltages and currents are processed directly in the appropriate modules.
>> In digital processing, analog signals are first converted into digital signals. After calculation of the manipulated variable in the microprocessor, the digital value is converted back into an analog value.

Although theoretically these two types of processing have to be dealt with very differently, there is no difference in the practical application of classical controllers.

Controlled System

The controlled system is the part of a machine or plant in which the controlled variable is to be maintained at the desired value and in which manipulated variables compensate for disturbance variables. Input variables to the controlled system include not only the manipulated variable, but also disturbance variables. Before a controller can be defined for a controlled system, the behaviour of the controlled system must be known. The control engineer is not interested in technical processes within the controlled system, but only in system behaviour.

Dynamic response of a system

The dynamic response of a system (also called time response) is an important aspect. It is the time characteristic of the output variable (controlled variable) for changes in the input variable. Particularly important is behaviour when the manipulated variable is changed. The control engineer must understand that nearly every system has a characteristic dynamic response.

Example 1

In the example of the water bath in Controlled System and Control Algorithm, a change in the steam valve setting will not immediately change the output variable temperature. Rather, the heat capacity of the entire water bath will cause the temperature to slowly "creep" to the new equilibrium (see Picture 1).

Picture 1: Time response of the controlled system "Water bath"

Example 2

In the example of a valve for volumetric flow control, the dynamic response is rapid. Here, a change in the valve setting has an immediate effect on flow rate so that the change in the volumetric flow rate output signal almost immediately follows the input signal for the change of the valve setting (see Picture 2).

Picture 2: Time response of the controlled system "Valve"

Description of the dynamic response of a controlled system

In the examples shown on Picture 1 and Picture 2, the time response was shown assuming a sudden change in input variable. This is a commonly used method of establishing the time response of system.

Step response

The response of a system to a sudden change of the input variable is called the step response. Every system can be characterized by its step response. The step response also allows a system to be described with mathematical formulas.

Dynamic response

This description of a system is also known as dynamic response. Picture 3 demonstrates this. Here the manipulated variable y is suddenly increased (see left diagram). The step response of the controlled variable x is a settling process with transient overshoot.

Picture 3: Step response

Equilibrium

Another characteristic of a system is its behaviour in equilibrium, the static behaviour.

Static behaviour

Static behaviour of a system is reached when none of the variables change with time. Equilibrium is reached when the system has settled. This state can be maintained for an unlimited time. The output variable is still dependent on the input variable – this dependence is shown by the characteristic of a system.

Example 3

The characteristic of the "Valve" system from our water bath example shows the relationship between volumetric flow and valve position (see Picture 4).

Picture 4: Characteristic curve of the "Valve" system


The characteristic shows whether the system is a linear or non-linear system. If the characteristic is a straight line, the system is linear. In our "Valve" system, the characteristic is non-linear. Many controlled systems that occur in practice are non-linear. However, they can often be approximated by a linear characteristic in the range in which they are operated.

ISA Symbology

The Instrumentation, Systems, and Automation Society (ISA) is one of the leading process control trade and standards organizations. The ISA has developed a set of symbols for use in engineering drawings and designs of control loops (ISA S5.1 instrumentation symbol specification). You should be familiar with ISA symbology so that you can demonstrate possible process control loop solutions on paper to your customer. Picture 1 shows a control loop using ISA symbology. Drawings of this kind are known as piping and instrumentation drawings (P&ID).

Picture 1: Control loop using ISA Symbology: Piping and Instrumentation Drawing

Symbols

In a P&ID, a circle represents individual measurement instruments, such as transmitters, sensors, and detectors (Picture 2).

Picture 2: Discrete Instruments (ISA Symbols)

A single horizontal line running across the center of the shape indicates that the instrument or function is located in a primary location (e.g., a control room). A double line indicates that the function is in an auxiliary location (e.g., an instrument rack). The absence of a line indicates that the function is field mounted, and a dotted line indicates that the function or instrument is inaccessible (e.g., located behind a panel board).
A square with a circle inside represents instruments that both display measurement readings and perform some control function (Picture 3). Many modern transmitters are equipped with microprocessors that perform control calculations and send control output signals to final control elements.

Picture 3: Shared Control/Display Elements (ISA Symbols)

Controllers

A hexagon represents computer functions, such as those carried out by a controller (Picture 4).

Picture 4: Computer Functions (Controllers)

PLCs

A square with a diamond inside represents PLCs (Picture 5).

Picture 5: PLCs

Valves

Two triangles with their apexes contacting each other (a “bow tie” shape) represent a valve in the piping. An actuator is always drawn above the valve (Picture 6).

Picture 6: Valves

Pumps

Directional arrows showing the flow direction represent a pump (Picture 7).

Picture 7: Pumps

Piping and Connections

Piping and connections are represented with several different symbols (Picture 8):

❑ A heavy solid line represents piping;
❑ A thin solid line represents process connections to instruments (e.g., impulse piping);
❑ A dashed line represents electrical signals (e.g., 4–20 mA connections);
❑ A slashed line represents pneumatic signal tubes;
❑ A line with circles on it represents data links.

Other connection symbols include capillary tubing for filled systems (e.g., remote diaphragm seals), hydraulic signal lines, and guided electromagnetic or sonic signals.

Picture 8: Piping and Connection Symbols

Identification Letters

Identification letters on the ISA symbols (e.g., TT for temperature transmitter) indicate:

❑ The variable being measured (e.g., flow, pressure, temperature);
❑ The device’s function (e.g., transmitter, switch, valve, sensor, indicator);
❑ Some modifiers (e.g., high, low, multifunction).

The table on Picture 9, shows the ISA identification letter designations.

The initial letter indicates the measured variable. The second letter indicates a modifier, readout, or device function. The third letter usually indicates either a device function or a modifier. For example, “FIC” on an instrument tag represents a flow indicating controller. “PT” represents a pressure transmitter. You can find identification letter symbology information on the ISA Web site at http://www.isa.org.

Picture 9: ISA Identification Letters

Tag Numbers

Numbers on P&ID symbols represent instrument tag numbers. Often these numbers are associated with a particular control loop (e.g., flow transmitter 123). See Picture 10.

Picture 10: Identification Letters and Tag Number

Components of Control Loops

This article describes the instruments, technologies, and equipment used to develop and maintain process control loops. In addition, this article describes how process control equipment is represented in technical drawings of control loops.

The goal of this article is to be able to:

❑ Describe the basic function of and, where appropriate, the basic method of operation for the following control loop components:
• Primary element/sensor
• Transducer
• Converter
• Transmitter
• Signal
• Indicator
• Recorder
• Controller
• Correcting element/final control element
• Actuator
❑ List examples of each type of control loop component listed above.
❑ State the advantages of 4–20 mA current signals when compared with other types of signals.
❑ List at least three types of final control elements, and for each one:
• Provide a brief explanation of its method of operation;
• Describe its impact on the control loop;
• List common applications in which it is used.
❑ Given a piping and instrumentation drawing (P&ID), correctly label the:
• Instrument symbols (e.g., control valves, pumps, transmitters);
• Location symbols (e.g., local, panel-front);
• Signal type symbols (e.g., pneumatic, electrical).
❑ Accurately interpret instrument letter designations used on P&IDs.

Control Loop Equipment and Technology

Previously, we described the basic elements of control as measurement, comparison, and adjustment. In practice, there are instruments and strategies to accomplish each of these essential tasks. In some cases, a single process control instrument, such as a modern pressure transmitter, may perform more than one of the basic control functions. Other technologies have been developed so that communication can occur among the components that measure, compare, and adjust.

Primary Elements - Sensors

In all cases, some kind of instrument is measuring changes in the process and reporting a process variable measurement. Some of the greatest ingenuity in the process control field is apparent in sensing devices. Because sensing devices are the first element in the control loop to measure the process variable, they are also called primary elements. Examples of primary elements include:

❑ Pressure sensing diaphragms, strain gauges, capacitance cells;
❑ Resistance temperature detectors (RTDs);
❑ Thermocouples;
❑ Orifice plates;
❑ Pitot tubes;
❑ Venturi tubes;
❑ Magnetic flow tubes;
❑ Coriolis flow tubes;
❑ Radar emitters and receivers;
❑ Ultrasonic emitters and receivers;
❑ Annubar flow elements;
❑ Vortex sheddar.

Primary elements are devices that cause some change in their property with changes in process fluid conditions that can then be measured. For example, when a conductive fluid passes through the magnetic field in a magnetic flow tube, the fluid generates a voltage that is directly proportional to the velocity of the process fluid. The primary element (magnetic flow tube) outputs a voltage that can be measured and used to calculate the fluid’s flow rate. With an RTD, as the temperature of a process fluid surrounding the RTD rises or falls, the electrical resistance of the RTD increases or decreases a proportional amount. The resistance is measured, and from this measurement, temperature is determined.

Transducers and Converters

A transducer is a device that translates a mechanical signal into an electrical signal. For example, inside a capacitance pressure device, a transducer converts changes in pressure into a proportional change in capacitance.

A converter is a device that converts one type of signal into another type of signal. For example, a converter may convert current into voltage or an analog signal into a digital signal. In process control, a converter used to convert a 4–20 mA current signal into a 3–15 psig pneumatic signal (commonly used by valve actuators) is called a current-to-pressure converter.

Transmitters

A transmitter is a device that converts a reading from a sensor or transducer into a standard signal and transmits that signal to a monitor or controller. Transmitter types include:

❑ Pressure transmitters;
❑ Flow transmitters;
❑ Temperature transmitters;
❑ Level transmitters;
❑ Analytic (O2 [oxygen], CO [carbon monoxide], and pH) transmitters.

Signals

There are three kinds of signals that exist for the process industry to transmit the process variable measurement from the instrument to a centralized control system:

1. Pneumatic signal
2. Analog signal
3. Digital signal

Pneumatic Signals

Pneumatic signals are signals produced by changing the air pressure in a signal pipe in proportion to the measured change in a process variable. The common industry standard pneumatic signal range is 3–15 psig. The 3 corresponds to the lower range value (LRV) and the 15 corresponds to the upper range value (URV). Pneumatic signalling is still common. However, since the advent of electronic instruments in the 1960s, the lower costs involved in running electrical signal wire through a plant as opposed to running pressurized air tubes has made pneumatic signal technology less attractive.

Analog Signals

The most common standard electrical signal is the 4–20 mA current signal. With this signal, a transmitter sends a small current through a set of wires. The current signal is a kind of gauge in which 4 mA represents the lowest possible measurement, or zero, and 20 mA represents the highest possible measurement. For example, imagine a process that must be maintained at 100 °C. An RTD temperature sensor and transmitter are installed in the process vessel, and the transmitter is set to produce a 4 mA signal when the process temperature is at 95 °C and a 20 mA signal when the process temperature is at 105 °C. The transmitter will transmit a 12 mA signal when the temperature is at the 100 °C setpoint. As the sensor’s resistance property changes in response to changes in temperature, the transmitter outputs a 4–20 mA signal that is proportionate to the temperature changes. This signal can be converted to a temperature reading or an input to a control device, such as a burner fuel valve. Other common standard electrical signals include the 1–5 V (volts) signal and the pulse output.

Digital Signals

Digital signals are the most recent addition to process control signal technology. Digital signals are discrete levels or values that are combined in specific ways to represent process variables and also carry other information, such as diagnostic information. The methodology used to combine the digital signals is referred to as protocol.
Manufacturers may use either an open or a proprietary digital protocol. Open protocols are those that anyone who is developing a control device can use. Proprietary protocols are owned by specific companies and may be used only with their permission. Open digital protocols include the HART® (highway addressable remote transducer) protocol, FOUNDATION™ Fieldbus, Profibus, DeviceNet, and the Modbus® protocol.

Indicators

While most instruments are connected to a control system, operators sometimes need to check a measurement on the factory floor at the measurement point. An indicator makes this reading possible. An indicator is a human-readable device that displays information about the process. Indicators may be as simple as a pressure or temperature gauge or more complex, such as a digital read-out device. Some indicators simply display the measured variable, while others have control buttons that enable operators to change settings in the field.

Recorders

A recorder is a device that records the output of a measurement devices. Many process manufacturers are required by law to provide a process history to regulatory agencies, and manufacturers use recorders to help meet these regulatory requirements. In addition, manufacturers often use recorders to gather data for trend analyses. By recording the readings of critical measurement points and comparing those readings over time with the results of the process, the process can be improved. Different recorders display the data they collect differently. Some recorders list a set of readings and the times the readings were taken; others create a chart or graph of the readings. Recorders that create charts or graphs are called chart recorders.

Controllers

A controller is a device that receives data from a measurement instrument, compares that data to a programmed setpoint, and, if necessary, signals a control element to take corrective action. Local controllers are usually one of the three types: pneumatic, electronic or programmable. Contollers also commonly reside in a digital control system (Picture 1).

Picture 1: Controllers


Controllers may perform complex mathematical functions to compare a set of data to setpoint or they may perform simple addition or subtraction functions to make comparisons. Controllers always have an ability to receive input, to perform a mathematical function with the input, and to produce an output signal. Common examples of controllers include:

❑ Programmable logic controllers (PLCs)—PLCs are usually computers connected to a set of input/output (I/O) devices. The computers are programmed to respond to inputs by sending outputs to maintain all processes at setpoint.
❑ Distributed control systems (DCSs)—DCSs are controllers that, in addition to performing control functions, provide readings of the status of the process, maintain databases and advanced man-machine-interface.

Correcting Elements - Final Control Elements

The correcting or final control element is the part of the control system that acts to physically change the manipulated variable. In most cases, the final control element is a valve used to restrict or cut off fluid flow, but pump motors, louvers (typically used to regulate air flow), solenoids, and other devices can also be final control elements.
Final control elements are typically used to increase or decrease fluid flow. For example, a final control element may regulate the flow of fuel to a burner to control temperature, the flow of a catalyst into a reactor to control a chemical reaction, or the flow of air into a boiler to control boiler combustion. In any control loop, the speed with which a final control element reacts to correct a variable that is out of setpoint is very important. Many of the technological improvements in final control elements are related to improving their response time.

Actuators

An actuator is the part of a final control device that causes a physical change in the final control device when signalled to do so. The most common example of an actuator is a valve actuator, which opens or closes a valve in response to control signals from a controller. Actuators are often powered pneumatically, hydraulically, or electrically. Diaphragms, bellows, springs, gears, hydraulic pilot valves, pistons, or electric motors are often parts of an actuator system.

Basic Terminology in Closed-loop Control

In Closed and Open Control Loops we look at the difference between open-loop and closed-loop control using the example of volumetric flow for a control valve. In addition we look at the basic principle of closed-loop control and basic terminology. Using this example, let’s take a closer look at closed-loop control terminology.

Controlled variable x

The aim of any closed-loop control is to maintain a variable at a desired value or on a desired-value curve. The variable to be controlled is known as the controlled variable x. In our example it is the volumetric flow.

Manipulated variable y

Automatic closed-loop control can only take place if the machine or system offers a possibility for influencing the controlled variable. The variable which can be changed to influence the controlled variable is called the manipulated variable y. In our example of volumetric flow, the manipulated variable is the drive current for the positioning solenoid.

Disturbance variable z

Disturbances occur in any controlled system. Indeed, disturbances are often the reason why a closed-loop control is required. In our example, the applied pressure changes the volumetric flow and thus requires a change in the control valve setting. Such influences are called disturbance variables z.
The controlled system is the part of a controlled machine or plant in which the controlled variable is to be maintained at the value of the reference variable. The controlled system can be represented as a system with the controlled variable as the output variable and the manipulated variable as the input variable. In the example of the volumetric flow control, the pipe system through which gas flows and the control valve formed the control system.

Reference variable w

The reference variable is also known as the set point. It represents the desired value of the controlled variable. The reference variable can be constant or may vary with time. The instantaneous real value of the controlled variable is called the actual value w.

Deviation xd

The result of a comparison of reference variable and controlled variable is the deviation xd:

xd = w - x

Control response

Control response indicates how the controlled system reacts to changes to the input variable. Determination of the control response is one of the aims of closed-loop control technology.

Controller

The controller has the task of holding the controlled variable as near as possible to the reference variable. The controller constantly compares the value of the controlled variable with the value of the reference variable. From this comparison and the control response, the controller determines and changes the value of the manipulating variable (see Picture 1).

Picture 1: Functional principle of a closed-loop control

Manipulating element and servo-drive

The manipulating element adjusts the controlled variable. The manipulating element is normally actuated by a special servo drive. A servo drive is required if it is not possible for the controller to actuate the manipulating element directly. In our example of volumetric flow control, the manipulating element is the control valve.

Measuring element

In order to make the controlled variable accessible to the controller, it must be measured by a measuring element (sensor, transducer) and converted into a physical variable that can be processed by the controller is an input.

Closed loop

The closed loop contains all components necessary for automatic closed-loop control (see Picture 2).

Picture 2: Block diagram of a control loop