Characteristics of Audio Signals

The test set

In order to compare test signals to realistic audio signals, it is necessary to define a test set of audio fragments. Due to the variation in volume in audio signals, the statistical parameters depend on the length of the time interval that is being analysed. Picture 1 shows the amplitude distribution of complete CD tracks. Compared to shorter fragments with constant volume (see Picture 2), we notice a somewhat larger spread and a clearly different shape which peaks around zero amplitude. This is a result of the sections with a lower volume. Now suppose we would use the distributions of Picture 1 to predict amplifier dissipation. Such a signal has a certain average power that has to be delivered by the amplifier, leading to a certain (predicted) average dissipation. During the loud passages, however, the amplifier has to deliver considerably more power, and when they last longer than the heat sink’s thermal time constant, the amplifier will overheat. Therefore, we have chosen audio fragments with constant volume. Of course it should be noted that "constant" is a relative measure, since the audio waveform itself is not constant. It is assumed that variations in less than seconds will not give rise to the problems described above.
There are chosen 80 fragments from various CD’s, including classical music, pop music, jazz, hard rock, house, heavily compressed music, and speech signals. The length of each fragment is between 3 and 12 s. The volume during each fragment is constant. All fragments were converted to mono and normalised to full scale, with the highest sample just clipping. The number of bits per sample was reduced to 8 to get smoother amplitude distributions. Because the fragments are normalised to full scale, this barely affects the sound impression.

Picture 1: Amplitude distributions (of 36 CD tracks, normalised to 1 at zero amplitude and then scaled to equal power)

Amplitude distribution

The amplitude distribution is determined by counting how many samples with a certain amplitude (28 = 256 levels) occur in one fragment. Picture 2 shows the amplitude distribution of all 80 fragments.

Picture 2: Amplitude distributions (of all fragments, normalised to 1 at zero amplitude and then scaled to equal power)


It confirms that the shape of the amplitude distribution is gaussian. There are a few exceptions, though. Firstly, one curve has two peaks symmetrically around zero amplitude. This is the distribution of a fragment hard-core house music, that contains purely synthesised sounds. Although this is an exceptional case, it shows the importance of realising that certain audio characteristics can differ significantly from the average case. Secondly, we see some very narrow curves. These are the distributions of speech signals. Due to the pauses inherent to spoken word, the distributions peak around zero amplitude.
When discussing amplitude distributions, it is useful to critically examine the Peak-to-Average Ratio (PAR). It is widely acknowledged as a signal property, and identical to the traditional crest factor. Expressed in dB’s, the PAR is defined as:

PAR = 20*log(U(t)max/URMS)


Picture 3 shows the PAR-s of all fragments. Roughly, it is between 10 dB and 20 dB, with an average of 15 dB. This means that "in order to be undistorted" the average audio fragment must have a power at least 12 dB below a full power sinewave.

Picture 3: Peak-to-Average ratios (of all fragments)


Often, the PAR is also used for calculating amplifier efficiencies, resulting in a certain efficiency for a certain PAR of the signal. In that case it is assumed that every fragment is amplified to a level just below clipping. The result is that the amplifier dissipation strongly depends on the PAR. The reason for this is, that the average power (or URMS) also varies considerably, since U(t)max is the clipping point of the amplifier and therefore constant. In Picture 2, however, it can be seen that, when scaled to equal power, the amplitude distributions are almost the same. U(t)max varies, but since the high amplitudes near U(t)max are unlikely to occur, they hardly effect the total dissipation of the amplifier. When a fragment with a large PAR is amplified to equal power as a fragment with a low PAR, there will be some clipping, but this is barely perceptible in normal listening conditions. Only when we increase the volume a lot, the sound quality degrades. Subjective listening tests show that the PAR can be made as small as 6dB before most fragments sound really bad through clipping. A PAR of 6dB means that the output power is half the maximum sine power. From the above we conclude the following: Audio fragments of constant volume generally have a gaussian amplitude distribution with an average PAR of 15dB. Concerning amplifier dissipation, average power is the most important variable, while the PAR does not play a significant role. Amplifier dissipation for gaussian signals must be tested up to half the full sine power.

Frequency distribution

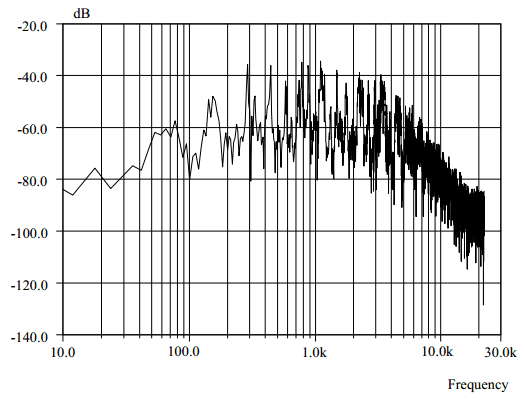
On the same audio fragments, a Fast Fourier Transform (FFT) was performed over the full length. A normal log-log bode plot of the frequency content (Picture 4) does not provide very useful information.

Picture 4: Traditional graph of a Fourier transform of a music fragment (Vertical scale dB’s are relative to full scale for measurement bandwidth 2/Tfragment)


Firstly, there is no need for a high accuracy, so it seems more logical to choose the vertical scale of the plot linear instead of logarithmic. Secondly, efficiency is a matter of power. When an amplifier has a better efficiency for certain frequencies, it is important to know how much power is present in those frequencies, not how much amplitude. So it’s more useful to square the amplitudes. Finally, the squared FFT gives the power of the frequencies in the signal. The frequencies are linearly spaced. With a logarithmic frequency axis, a temptation exists to overemphasise the lower frequencies because they are relatively enlarged. A linear frequency axis might seem a logical choice, but since pitch perception is logarithmic in nature (every octave higher equals a factor two), it is preferable to use a logarithmic axis, and plot the sum of the squared Fourier coefficients. An extra advantage is that the summation smoothens the curve.
Presented in this way, the frequency distribution is a line that starts at (almost) power = 0 at 20 Hz, climbing to power = 1 at 20 kHz. The frequency distributions of all fragments are shown on Picture 5. The average fragment is S-shaped, with a mid-frequency part corresponding to a straight line between (50 Hz, 0) and (3 kHz, 1). This does not come as a surprise when we realise that the notes in a musical scale are fixed factors in frequency apart, in which case a linear frequency distribution requires all notes to be equally loud. In Picture 5, the fragments with much power in the lower frequencies have a house beat or a contrabass. The fragments with much power in the higher frequencies mostly have electric guitars or synthesisers. One fragment in particular stands out because it contains much more high frequencies than the others. It is the intro of Melissa Etheridge’s "Like the way I do", containing a guitar and a tambourine.

Picture 5: Frequency distribution (of all audio fragments)